题目内容
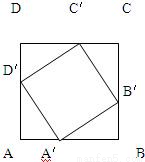
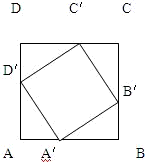
已知ABCD，A'B'C'D'都是正方形（如图），而A'、B'、C'、D'分别把AB、BC、CD、DA分为m：n，设AB=1．（1）求A'B'C'D'的面积；
（2）求证A'B'C'D'的面积不小于
．
【答案】分析：（1）由题意设AA'=mt，A'B=nt，通过
．推出A'B'C'D'的面积的表达式；
（2）利用配方把（1）的面积转化为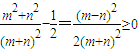
，从而证明A'B'C'D'的面积不小于
．
解答：解（1）：设AA'=mt，A'B=nt
又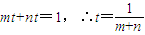
．
在直角△D'AA'中，
D'A'2=D'A2+AA'2=m2t2+n2t2
=（m2+n2）t2
而正方形A'B'C'D'的面积=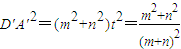
．
（2）证明：∵
∴
．
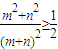点评：本题是基础题，考查平面几何的知识点，正方形的面积的求法，作差法证明A'B'C'D'的面积不小于
．是本题的难点，注意把握．
．推出A'B'C'D'的面积的表达式；（2）利用配方把（1）的面积转化为
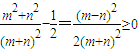，从而证明A'B'C'D'的面积不小于．解答：解（1）：设AA'=mt，A'B=nt
又
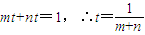．在直角△D'AA'中，
D'A'2=D'A2+AA'2=m2t2+n2t2
=（m2+n2）t2
而正方形A'B'C'D'的面积=
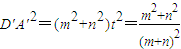．（2）证明：∵
∴
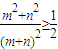．点评：本题是基础题，考查平面几何的知识点，正方形的面积的求法，作差法证明A'B'C'D'的面积不小于
．是本题的难点，注意把握． 
练习册系列答案
相关题目
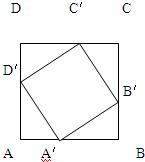已知ABCD，A'B'C'D'都是正方形（如图），而A'、B'、C'、D'分别把AB、BC、CD、DA分为m：n，设AB=1．
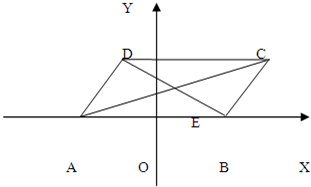已知□ABCD，A（-2，0），B（2，0），且|AD|=2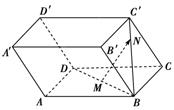
已知ABCD，A'B'C'D'都是正方形（如图），而A'、B'、C'、D'分别把AB、BC、CD、DA分为m：n，设AB=1．
．