题目内容
【题目】若图,在三棱柱 ![]() 中,平面
中,平面 ![]() 平面
平面 ![]() ,且
,且 ![]() 和
和 ![]() 均为正三角形.
均为正三角形.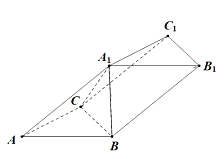
(1)在 ![]() 上找一点
上找一点 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ,并说明理由.
,并说明理由.
(2)若 ![]() 的面积为
的面积为 ![]() ,求四棱锥
,求四棱锥 ![]() 的体积.
的体积.
【答案】
(1)解: ![]() 为
为 ![]() 的中点时,
的中点时, ![]() 平面
平面 ![]() ,
,
如图,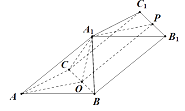
取 ![]() 的中点
的中点 ![]() 的中点
的中点 ![]() ,连结
,连结 ![]() ,
,
在三棱柱 ![]() 中,
中, ![]() ,
,
所以四边形 ![]() 为平行四边形,
为平行四边形, ![]() ,
,
由已知, ![]() 为正三角形,所以
为正三角形,所以 ![]() ,
,
因为 ![]() 平面
平面 ![]() ,平面
,平面 ![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]()
(2)解:设 ![]() 的边长为
的边长为 ![]() ,则
,则 ![]() ,
,
所以 ![]() ,
,
因为三棱柱 ![]() 的体积为三棱锥
的体积为三棱锥 ![]() 体积的
体积的 ![]() 倍,
倍,
所以四棱锥 ![]() 的体积等于三棱锥
的体积等于三棱锥 ![]() 体积的
体积的 ![]() 倍,
倍,
即 ![]() .
.
【解析】(1)根据题意结合已知条件作出辅助线即可得出线线平行进而得到四边形 A1 A O P 为平行四边形故有 A1 P / / A O 再由正三角形的性质得到 A O ⊥ B C再由面面垂直的性质得到线面垂直。(2)结合题意可知四棱锥 A1 B C C1 B1的体积等于三棱锥 A1 A B C 体积的 2 倍代入数值到三棱锥体积的公式求出结果即可。
【考点精析】根据题目的已知条件,利用平面与平面垂直的性质的相关知识可以得到问题的答案,需要掌握两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目