题目内容
若函数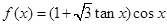 ,
,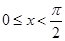 ,则
,则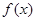 的最大值为
的最大值为
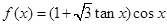 ,
,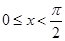 ,则
,则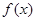 的最大值为
的最大值为| A.1 | B.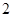 | C.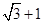 | D.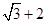 |
B
分析:先对函数f(x)=(1+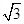 tanx)cosx进行化简,再根据x的范围求最大值.
tanx)cosx进行化简,再根据x的范围求最大值.
解:f(x)=(1+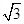 tanx)cosx=cosx+
tanx)cosx=cosx+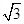 sinx=2sin(x+
sinx=2sin(x+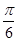 )
)
∵0≤x<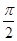 ,∴
,∴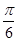 ≤x+
≤x+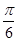 <
<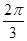
∴f(x)∈[1,2]
故选B.
点评:本题主要考查三角函数求最值问题.一般都是先将函数式进行化简再求值,这里一定要注意角的取值范围.
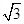 tanx)cosx进行化简,再根据x的范围求最大值.
tanx)cosx进行化简,再根据x的范围求最大值.解:f(x)=(1+
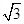 tanx)cosx=cosx+
tanx)cosx=cosx+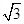 sinx=2sin(x+
sinx=2sin(x+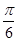 )
)∵0≤x<
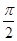 ,∴
,∴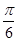 ≤x+
≤x+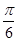 <
<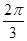
∴f(x)∈[1,2]
故选B.
点评:本题主要考查三角函数求最值问题.一般都是先将函数式进行化简再求值,这里一定要注意角的取值范围.

练习册系列答案
相关题目
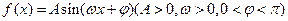 的一个周期的图象,如图(1)求
的一个周期的图象,如图(1)求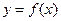 的解析式(2)若函数
的解析式(2)若函数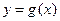 与
与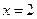 对称,求
对称,求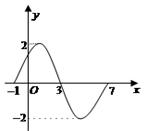
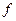 (
(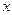 )=2
)=2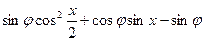 (
(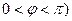 在
在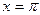 处
处 取得最小值.
取得最小值.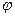 的值
的值 ;
;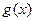 和函数
和函数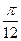 ,
,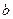 )对称,求函数
)对称,求函数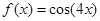 ,
,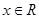 是
是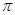 的偶函数
的偶函数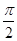 的偶函数
的偶函数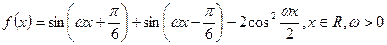
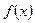 的值域
的值域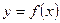 的图像与直线
的图像与直线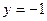 的两个相邻交点间的距离为
的两个相邻交点间的距离为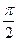 ,求函数
,求函数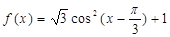 的最小正周期是( )
的最小正周期是( )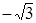
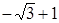
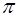
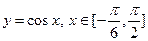 的值域是 ▲
的值域是 ▲ 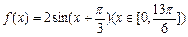 的图象与直线y=m的三个交点的横坐标分别为
的图象与直线y=m的三个交点的横坐标分别为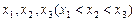 ,那么
,那么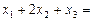 .
.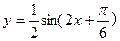 的单增区间是___________.
的单增区间是___________.