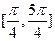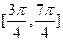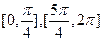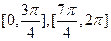题目内容
(本小题满分13分)
设函数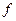 (
(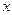 )=2
)=2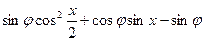 (
(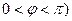 在
在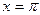 处
处 取得最小值.
取得最小值.
(Ⅰ)求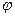 的值
的值 ;
;
(Ⅱ)已知函数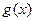 和函数
和函数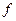 (
(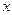 )关于点(
)关于点(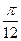 ,
,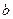 )对称,求函数
)对称,求函数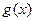 的单调增区间.
的单调增区间.
设函数
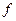 (
(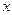 )=2
)=2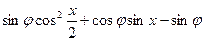 (
(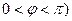 在
在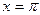 处
处 取得最小值.
取得最小值.(Ⅰ)求
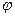 的值
的值 ;
;(Ⅱ)已知函数
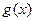 和函数
和函数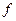 (
(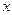 )关于点(
)关于点(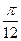 ,
,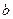 )对称,求函数
)对称,求函数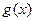 的单调增区间.
的单调增区间.解: (Ⅰ)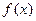 =2
=2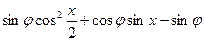
=2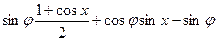 …………………2分
…………………2分
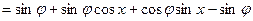
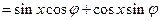
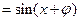 . …………………5分
. …………………5分
因为函数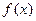 在
在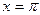 处取最小值,所以
处取最小值,所以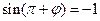 . ………………6分
. ………………6分
由诱导公式知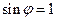 ,因为
,因为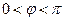 ,所以
,所以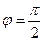 .
.
所以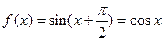 . ………………………………7分
. ………………………………7分
(Ⅱ)因为函数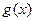 和函数
和函数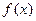 关于点(
关于点(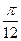 ,
,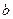 )对称,
)对称,
所以g(x)=2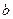 -
-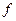 (
(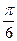 -x)=2
-x)=2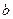 -cos(
-cos(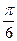 -x) =2
-x) =2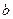 -cos(x-
-cos(x-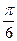 ), ………10分
), ………10分
由不等式 ,得到
,得到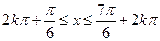 ,
,
所以函数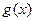 的单调增区间为
的单调增区间为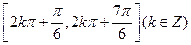 . …………13分
. …………13分
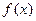 =2
=2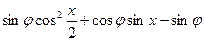
=2
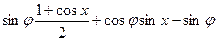 …………………2分
…………………2分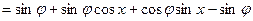
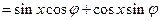
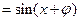 . …………………5分
. …………………5分因为函数
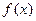 在
在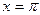 处取最小值,所以
处取最小值,所以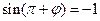 . ………………6分
. ………………6分由诱导公式知
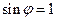 ,因为
,因为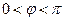 ,所以
,所以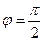 .
.所以
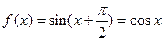 . ………………………………7分
. ………………………………7分
(Ⅱ)因为函数
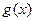 和函数
和函数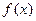 关于点(
关于点(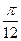 ,
,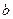 )对称,
)对称,所以g(x)=2
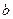 -
-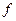 (
(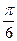 -x)=2
-x)=2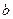 -cos(
-cos(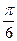 -x) =2
-x) =2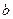 -cos(x-
-cos(x-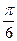 ), ………10分
), ………10分由不等式
 ,得到
,得到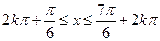 ,
,所以函数
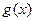 的单调增区间为
的单调增区间为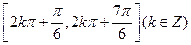 . …………13分
. …………13分略

练习册系列答案
相关题目
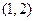 ,b=
,b=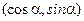 ,设m=a+tb(t为实数).
,设m=a+tb(t为实数).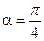 ,求当|m|取最小值时实数t的值;
,求当|m|取最小值时实数t的值;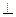 b,问:是否存在实数t,使得向量a-b和向量m的夹角为
b,问:是否存在实数t,使得向量a-b和向量m的夹角为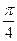 ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由.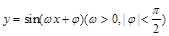 的图象的一部分
的图象的一部分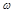 、
、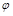 的值分别为()
的值分别为()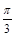
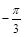
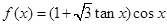 ,
,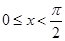 ,则
,则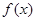 的最大值为
的最大值为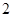
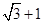
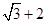
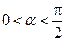 ,
,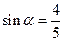 .
.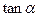 的值;
的值; 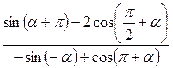 的值.
的值.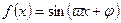 的图像向右平移
的图像向右平移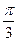 个单位。若所得图象与原图象重合,则
个单位。若所得图象与原图象重合,则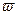 的值不可能等于 ( )
的值不可能等于 ( )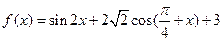 的最小值是
的最小值是 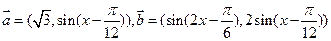 ,函数
,函数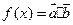
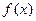 的最小正周期;
的最小正周期;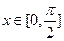 时,求函数
时,求函数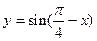 在区间
在区间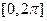 上的单调递减区间是 ( )
上的单调递减区间是 ( )