题目内容
14.已知复数$z=\frac{2i}{1-i}$,若|z|2+az+b=1-i.(Ⅰ)求$\overline z$;
(Ⅱ)求实数a,b的值.
分析 (I)利用复数的运算法则、共轭复数的定义即可得出.
(II)利用复数的运算法则、复数相等即可得出.
解答 解:( I)$z=\frac{2i(1+i)}{(1-i)(1+i)}=i(1+i)=-1+i$.
∴$\overline{z}$=-1-i.
( II)把z=-1+i代入|z|2+az+b=1-i,
即|-1+i|2+a(-1+i)+b=1-i,
得(-a+b+2)+ai=1-i.
∴$\left\{\begin{array}{l}-a+b+2=1\\ a=-1\end{array}\right.$,解得$\left\{\begin{array}{l}a=-1\\ b=-2\end{array}\right.$.
∴实数a,b的值分别为-1,-2.
点评 本题考查了复数的运算法则、共轭复数的定义、复数相等,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知△ABC中的内角为A,B,C,重心为G,若2sinA$\overrightarrow{GA}$+$\sqrt{3}$sinB$\overrightarrow{GB}$+3sinC$\overrightarrow{GC}$=$\overrightarrow{0}$,则cosB=( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
2.复平面上表示复数z=1-i(i为虚数单位)的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知a>b≥2,现有下列不等式:
①b2<3b-a;②a3+b3>a2b+ab2;③ab>a+b;④$\frac{1}{2}$+$\frac{2}{ab}$>$\frac{1}{a}$+$\frac{1}{b}$.
其中正确的是( )
①b2<3b-a;②a3+b3>a2b+ab2;③ab>a+b;④$\frac{1}{2}$+$\frac{2}{ab}$>$\frac{1}{a}$+$\frac{1}{b}$.
其中正确的是( )
| A. | ②④ | B. | ①④ | C. | ②③ | D. | ①③ |
19.抛物线x2=2y的焦点到准线的距离是( )
| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
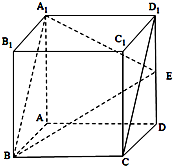 如图所示,正方体ABCD-A1B1C1D1的棱长为1,E是棱DD1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,E是棱DD1的中点.