题目内容
18.已知函数$f(x)=\left\{{\begin{array}{l}{x{e^x}+\frac{1}{e},x≤0}\\{{x^2}-2x,x>0}\end{array}}\right.$,若函数y=f(f(x)-a)有四个零点,则实数a的所有可能取值构成的集合是(1,1+$\frac{1}{e}$).分析 先运用导数求得函数单调区间,并作出图象,再根据图象列出函数有4个零点所需的条件.
解答  解:知函数$f(x)=\left\{{\begin{array}{l}{x{e^x}+\frac{1}{e},x≤0}\\{{x^2}-2x,x>0}\end{array}}\right.$,函数性质分段讨论如下:
解:知函数$f(x)=\left\{{\begin{array}{l}{x{e^x}+\frac{1}{e},x≤0}\\{{x^2}-2x,x>0}\end{array}}\right.$,函数性质分段讨论如下:
①当x>0时,f(x)=x2-2x=(x-1)2-1,最小值为-1,
②当x≤0时,令f'(x)=(x+1)ex=0,解得x=-1,
所以,x∈(-∞,-1)函数递减,(-1,0)函数递增,
且f(0)=$\frac{1}{e}$,x→-∞时,f(x)→$\frac{1}{e}$,
综合以上分析,作出函数图象,如右图.
由图可知,函数y=f(x)有两个零点,x=-1和x=2,----(*)
再考察函数y=f[f(x)-a]的零点,
由(*)可知,f(x)-a=-1或f(x)-a=2,
即f(x)=a-1或f(x)=a+2,根据题意,这两个方程共有四个根,
结合函数图象,a-1∈(0,$\frac{1}{e}$),解得,a∈(1,1+$\frac{1}{e}$),
故填:(1,1+$\frac{1}{e}$).
点评 本题主要考查了函数零点的判定,以及函数的图象和性质,并运用导数确定函数的单调区间,结合函数图象得出零点个数,具有一定的综合性,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.(文)已知α∈R,sinα+2cosα=$\frac{\sqrt{10}}{2}$,则$\frac{(sinα+cosα+1)(sinα+cosα-1)}{(sinα-cosα)(sinα+cosα)}$=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
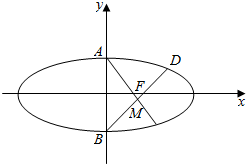 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,F为椭圆的右焦点,点A,B分别为椭圆的上下顶点,过点B作AF的垂线,垂足为M.