题目内容
9.设正实数x,y,z满足x2-3xy+4y2-z=0,则$\frac{z}{xy}$的最小值为1.分析 根据条件x2-3xy+4y2-z=0分离出z=x2-3xy+4y2并代入$\frac{z}{xy}$,再裂项,最后运用基本不等式求其最小值.
解答 解:∵x2-3xy+4y2-z=0,
∴z=x2-3xy+4y2,又因为x,y,z为正实数,
因此,$\frac{z}{xy}$=$\frac{x^2-3xy+4y^2}{xy}$=$\frac{x}{y}$+$\frac{4y}{x}$-3,
根据基本不等式,$\frac{x}{y}$+$\frac{4y}{x}$≥2$\sqrt{\frac{x}{y}•\frac{4y}{x}}$=4,当且仅当x=2y时,取“=”,
所以,$\frac{x}{y}$+$\frac{4y}{x}$-3∈[1,+∞),
所以,$\frac{z}{xy}$的最小值为1,
故填:1.
点评 本题主要考查了基本不等式在求最值中的应用,涉及到整体代换,裂项等运算技巧,属于中档题.

练习册系列答案
相关题目
17.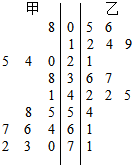 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间
各自的点击量,得到如图所示的统计图,根据统计图,甲、乙二者的中位数中较大那个为( )
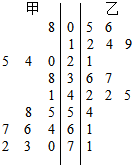 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00间各自的点击量,得到如图所示的统计图,根据统计图,甲、乙二者的中位数中较大那个为( )
| A. | 55 | B. | 56.5 | C. | 37 | D. | 36.5 |
4.在一段时间内,某种商品的价格x(单位:元)与需求量y(单位:件)之间的一组数据如表:
如果y与x具有线性相关关系,求y与x的回归直线方程.$\frac{∧}{b}$
参考公式:$\frac{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n({\overline{x})}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$;直线方程$\widehat{y}=\widehat{b}x+\widehat{a}$.
| 价格 | 14 | 16 | 18 | 20 | 22 |
| 需求量 | 12 | 10 | 12 | 5 | 3 |
参考公式:$\frac{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n({\overline{x})}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$;直线方程$\widehat{y}=\widehat{b}x+\widehat{a}$.