题目内容
已知函数
（Ⅰ）求函数f (x)的定义域
（Ⅱ）确定函数f (x)在定义域上的单调性，并证明你的结论.
（Ⅲ）若x>0时
恒成立，求正整数k的最大值.
（Ⅰ）
（Ⅱ）在（－1，0）和（0，+
）上都是减函数
（Ⅲ）k的最大值为3
解析:
（1）定义域
（2）
单调递减。
当
，
令
故
在（-1，0）上是减函数即 
故此时
在（－1，0）和（0，+
）上都是减函数
（3）当x>0时，
恒成立，令
又k为正整数，∴k的最大值不大于3
下面证明当k=3时 
恒成立
当x>0时 
恒成立 令
则
当
∴当
取得最小值
当x>0时 恒成立 因此正整数k的最大值为3
练习册系列答案
相关题目
，如果满足；对任意
，存在常数
，都有
成立，则称
，
当
时，求函数
上的值域，并判断函数
上是以3为上界函数值，求实数
的取值范围；若
，求函数
在
上的上界T的取值范围。
的定义域；
为何值时，函数值大于1.
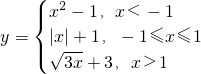编写一程序求函数值．
编写一程序求函数值．
编写一程序求函数值．