题目内容
已知函数
(1)求 的定义域;
的定义域;
(2)当 为何值时,函数值大于1.
为何值时,函数值大于1.
【答案】
(1)当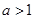 时,定义域为
时,定义域为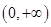 ,当
,当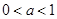 时,定义域为
时,定义域为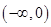 .
.
(2)当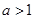 时,
时,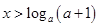 时,函数值大于1;
时,函数值大于1;
当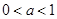 时,
时,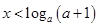 时,函数值大于1.
时,函数值大于1.
【解析】
试题分析:(1)由已知,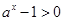 ,即
,即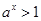 ,当
,当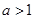 时,
时,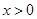 ,当
,当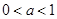 时,
时,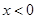 .
.
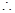 当
当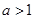 时,定义域为
时,定义域为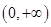 ,当
,当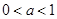 时,定义域为
时,定义域为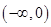 .
6分
.
6分
(2)当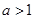 时,由
时,由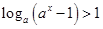 得
得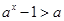 ,即
,即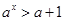 ,
,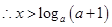 .
.
当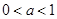 时,由
时,由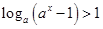 得
得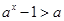 ,即
,即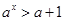 ,
,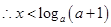 .
.
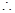 当
当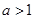 时,
时,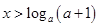 时,函数值大于1;
时,函数值大于1;
当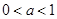 时,
时,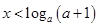 时,函数值大于1.
14分
时,函数值大于1.
14分
考点:本题主要考查指数函数、对数函数的图象和性质,分类讨论思想。
点评:中档题,研究指数函数、对数函数的性质,首先要关注“底数”的取值范围,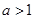 时,是增函数,
时,是增函数,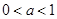 时,是减函数。复合函数的单调性,遵循“内外层函数,同增异减”。本题利用分类讨论思想,注意要“不重不漏”。
时,是减函数。复合函数的单调性,遵循“内外层函数,同增异减”。本题利用分类讨论思想,注意要“不重不漏”。

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目

 的最小正周期及
的最小正周期及 上的图象.
上的图象. ,
,
 的单调区间;
的单调区间;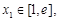 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。 知函数
知函数
 的定义域;
的定义域; 上是减函数.
上是减函数. .
. 的最小正周期;
的最小正周期; 上的最大值和最小值以及取得最大值、最小值时x的值.
上的最大值和最小值以及取得最大值、最小值时x的值.