题目内容
已知点A(1,0),B(0,1)和互不相同的点P1,P2,P3,…,Pn,…,满足 ,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.
,其中{an}、{bn}分别为等差数列和等比数列,O为坐标原点,若P1是线段AB的中点.(Ⅰ)求a1,b1的值;
(Ⅱ)点P1,P2,P3,…,Pn,…能否共线?证明你的结论;
(Ⅲ)证明:对于给定的公差不零的{an},都能找到唯一的一个{bn},使得P1,P2,P3,…,Pn,…,都在一个指数函数的图象上.
【答案】分析:(Ⅰ)P1是线段AB的中点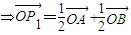 ,
,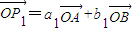 ,且
,且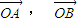 不共线,由平面向量基本定理,能求出a1,b1的值.
不共线,由平面向量基本定理,能求出a1,b1的值.
(Ⅱ) 由 ,设{an}的公差为d,{bn}的公比为q,则由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不会同时成立;若d=0,则
,设{an}的公差为d,{bn}的公比为q,则由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不会同时成立;若d=0,则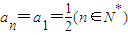 ,所以P1,P2,P3,…,Pn,…都在直线
,所以P1,P2,P3,…,Pn,…都在直线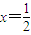 上.由此能求出当d≠0且q≠1时,P1,P2,P3,…,Pn,…不共线.
上.由此能求出当d≠0且q≠1时,P1,P2,P3,…,Pn,…不共线.
(Ⅲ)设Pn(an,bn)都在指数函数y=ax(a>0,a≠1)的图象上,则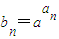
 .令n=1,则
.令n=1,则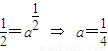 ,于是,
,于是,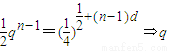 有唯一解
有唯一解 .由此能够得到当对于给定的{an},都能找到唯一的一个{bn},使得P1,P2,P3,…,Pn,…,都在指数函数
.由此能够得到当对于给定的{an},都能找到唯一的一个{bn},使得P1,P2,P3,…,Pn,…,都在指数函数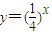 的图象上.
的图象上.
解答:解:(Ⅰ)P1是线段AB的中点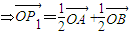 …(1分)
…(1分)
又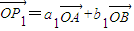 ,且
,且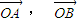 不共线,
不共线,
由平面向量基本定理,知: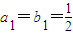 …(3分)
…(3分)
(Ⅱ) 由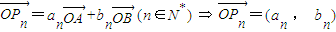
设{an}的公差为d,{bn}的公比为q,则由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不会同时成立; (4分)
若d=0,则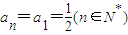 ,⇒P1,P2,P3,…,Pn,…都在直线
,⇒P1,P2,P3,…,Pn,…都在直线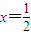 上; …(5分)
上; …(5分)
若q=1,则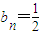 为常数列,⇒P1,P2,P3,…,Pn,…都在直线
为常数列,⇒P1,P2,P3,…,Pn,…都在直线 上; …(6分)
上; …(6分)
若d≠0且q≠1,P1,P2,P3,…,Pn,…共线?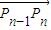 =(an-an-1,bn-bn-1)与
=(an-an-1,bn-bn-1)与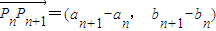 共线(n>1,n∈N*)?(an-an-1)(bn+1-bn)-(an+1-an)(bn-bn-1)=0?d(bn+1-bn)-d(bn-bn-1)=0?(bn+1-bn)=(bn-bn-1)?q=1与q≠1矛盾,
共线(n>1,n∈N*)?(an-an-1)(bn+1-bn)-(an+1-an)(bn-bn-1)=0?d(bn+1-bn)-d(bn-bn-1)=0?(bn+1-bn)=(bn-bn-1)?q=1与q≠1矛盾,
∴当d≠0且q≠1时,P1,P2,P3,…,Pn,…不共线. …(9分)
(Ⅲ)设Pn(an,bn)都在指数函数y=ax(a>0,a≠1)的图象上,则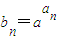
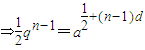 (10分)
(10分)
令n=1,则 ,…(11分)
,…(11分)
于是, 有唯一解
有唯一解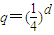 ,…(13分)
,…(13分)
由于d≠0,⇒q≠1,从而满足条件“P1,P2,P3,…,Pn,…互不相同”.
∴当对于给定的{an},都能找到唯一的一个{bn},
使得P1,P2,P3,…,Pn,…,都在指数函数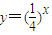 的图象上.…(14分)
的图象上.…(14分)
点评:本题考查数列与解析几何间的关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
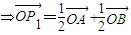 ,
,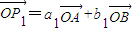 ,且
,且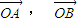 不共线,由平面向量基本定理,能求出a1,b1的值.
不共线,由平面向量基本定理,能求出a1,b1的值.(Ⅱ) 由
 ,设{an}的公差为d,{bn}的公比为q,则由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不会同时成立;若d=0,则
,设{an}的公差为d,{bn}的公比为q,则由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不会同时成立;若d=0,则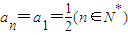 ,所以P1,P2,P3,…,Pn,…都在直线
,所以P1,P2,P3,…,Pn,…都在直线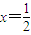 上.由此能求出当d≠0且q≠1时,P1,P2,P3,…,Pn,…不共线.
上.由此能求出当d≠0且q≠1时,P1,P2,P3,…,Pn,…不共线. (Ⅲ)设Pn(an,bn)都在指数函数y=ax(a>0,a≠1)的图象上,则
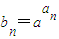
 .令n=1,则
.令n=1,则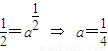 ,于是,
,于是,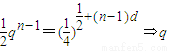 有唯一解
有唯一解 .由此能够得到当对于给定的{an},都能找到唯一的一个{bn},使得P1,P2,P3,…,Pn,…,都在指数函数
.由此能够得到当对于给定的{an},都能找到唯一的一个{bn},使得P1,P2,P3,…,Pn,…,都在指数函数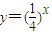 的图象上.
的图象上.解答:解:(Ⅰ)P1是线段AB的中点
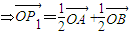 …(1分)
…(1分)又
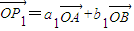 ,且
,且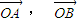 不共线,
不共线,由平面向量基本定理,知:
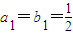 …(3分)
…(3分)(Ⅱ) 由
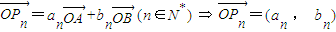
设{an}的公差为d,{bn}的公比为q,则由于P1,P2,P3,…,Pn,…互不相同,所以d=0,q=1不会同时成立; (4分)
若d=0,则
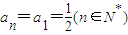 ,⇒P1,P2,P3,…,Pn,…都在直线
,⇒P1,P2,P3,…,Pn,…都在直线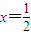 上; …(5分)
上; …(5分)若q=1,则
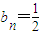 为常数列,⇒P1,P2,P3,…,Pn,…都在直线
为常数列,⇒P1,P2,P3,…,Pn,…都在直线 上; …(6分)
上; …(6分)若d≠0且q≠1,P1,P2,P3,…,Pn,…共线?
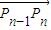 =(an-an-1,bn-bn-1)与
=(an-an-1,bn-bn-1)与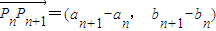 共线(n>1,n∈N*)?(an-an-1)(bn+1-bn)-(an+1-an)(bn-bn-1)=0?d(bn+1-bn)-d(bn-bn-1)=0?(bn+1-bn)=(bn-bn-1)?q=1与q≠1矛盾,
共线(n>1,n∈N*)?(an-an-1)(bn+1-bn)-(an+1-an)(bn-bn-1)=0?d(bn+1-bn)-d(bn-bn-1)=0?(bn+1-bn)=(bn-bn-1)?q=1与q≠1矛盾,∴当d≠0且q≠1时,P1,P2,P3,…,Pn,…不共线. …(9分)
(Ⅲ)设Pn(an,bn)都在指数函数y=ax(a>0,a≠1)的图象上,则
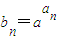
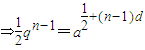 (10分)
(10分)令n=1,则
 ,…(11分)
,…(11分)于是,
 有唯一解
有唯一解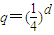 ,…(13分)
,…(13分)由于d≠0,⇒q≠1,从而满足条件“P1,P2,P3,…,Pn,…互不相同”.
∴当对于给定的{an},都能找到唯一的一个{bn},
使得P1,P2,P3,…,Pn,…,都在指数函数
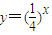 的图象上.…(14分)
的图象上.…(14分)点评:本题考查数列与解析几何间的关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.