题目内容
如果直线y=kx+1与圆x2+y2+kx+my-4=0相交于M、N两点,且点M、N关于直线x+y=0对称,动点P(a,b)在不等式组
表示的平面区域的内部及边界上运动,则
(1)不等式组所确定的平面区域的面积为1;
(2)使得目标函数z=b-a取得最大值的最优解有且仅有一个;
(3)目标函数ω=
的取值范围是[-2,2];
(4)目标函数p=a2+b2-2b+1的最小值是
.
上述说法中正确的是
|
(1)不等式组所确定的平面区域的面积为1;
(2)使得目标函数z=b-a取得最大值的最优解有且仅有一个;
(3)目标函数ω=
| b-2 |
| a-1 |
(4)目标函数p=a2+b2-2b+1的最小值是
| 1 |
| 2 |
上述说法中正确的是
(1)(4)
(1)(4)
(写出所有正确选项)分析:由M与N关于x+y=0对称得到直线y=kx+1与x+y=0垂直,利用两直线垂直时斜率的乘积为-1,得到k的值;设出M与N的坐标,然后联立y=x+1与圆的方程,消去y得到关于x的一元二次方程,根据韦达定理得到两横坐标之和的关于m的关系式,再根据MN的中点在x+y=0上得到两横坐标之和等于-1,列出关于m的方程,求出方程的解得到m的值,把k的值和m的值代入不等式组,在数轴上画出相应的平面区域,求出面积及相应的目标函数的最值即得.如对于(3),先由条件求出k=1,m=-1,再画出对应的平面区域,把ω=
看成平面区域内的点与(1,2)连线的斜率,利用图形可得结论.
| b-2 |
| a-1 |
解答: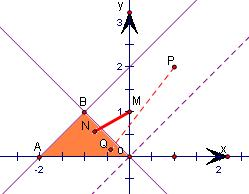 解:∵M、N两点,关于直线x+y=0对称,
解:∵M、N两点,关于直线x+y=0对称,
∴k=1,又圆心(-
,-
)在直线x+y=0上
∴-
-
=0
∴m=-1
∴原不等式组变为
作出不等式组表示的平面区域,
(1)△AOB为不等式所表示的平面区域,
联立
解得B(-1,1),A(-2,0),
所以S△AOB=
×|-2|×|-1|=1.
故(1)正确;
(2)作出目标函数z=b-a平行的直线,将其平移
当直线z=b-a过直线x-y+2=0上的任一点时,z最大,
故(2)错;
(3)如图
又因为ω=
表示点P(a,b)与点(1,2)连线的斜率.
故当过点B(-1,1)时,ω=
取最小值-
.
当过O(0,0)时,ω=
取最大值2.
故答案为:[-
,2].故(3)错;
(4)p=a2+b2-2b+1=a2+(b-1)2-表示区域内的点N到点M(0,1)的距离的平方,
由图得:只有当过M作直线x+y=0的垂线时,M(0,1)到平面区域内任一点的距离才最小.
而M与直线x+y=0的距离为:d=
=
.
∴|d|2=
.即目标函数p=a2+b2-2b+1的最小值是
.
故(4)正确.
故答案为:(1),(4).
 解:∵M、N两点,关于直线x+y=0对称,
解:∵M、N两点,关于直线x+y=0对称,∴k=1,又圆心(-
| k |
| 2 |
| m |
| 2 |
∴-
| k |
| 2 |
| m |
| 2 |
∴m=-1
∴原不等式组变为
|
(1)△AOB为不等式所表示的平面区域,
联立
|
所以S△AOB=
| 1 |
| 2 |
故(1)正确;
(2)作出目标函数z=b-a平行的直线,将其平移
当直线z=b-a过直线x-y+2=0上的任一点时,z最大,
故(2)错;
(3)如图
又因为ω=
| b-2 |
| a-1 |
故当过点B(-1,1)时,ω=
| b-2 |
| a-1 |
| 1 |
| 2 |
当过O(0,0)时,ω=
| b-2 |
| a-1 |
故答案为:[-
| 1 |
| 2 |
(4)p=a2+b2-2b+1=a2+(b-1)2-表示区域内的点N到点M(0,1)的距离的平方,
由图得:只有当过M作直线x+y=0的垂线时,M(0,1)到平面区域内任一点的距离才最小.
而M与直线x+y=0的距离为:d=
| |0+1| | ||
|
| 1 | ||
|
∴|d|2=
| 1 |
| 2 |
| 1 |
| 2 |
故(4)正确.
故答案为:(1),(4).
点评:本题是简单的线性规划与直线和直线以及直线与圆的位置关系的一道综合题,是对知识的综合考查.利用直线斜率的几何意义,求可行域中的点与(1,2)的斜率ω=
的取值范围.
| b-2 |
| a-1 |

练习册系列答案
相关题目