题目内容
如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N两点,且M、N关于直线x+y=0对称,则不等式组:
表示的平面区域的面积是( )
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
分析:由M与N关于x+y=0对称得到直线y=kx+1与x+y=0垂直,利用两直线垂直时斜率的乘积为-1,得到k的值;设出M与N的坐标,然后联立y=x+1与圆的方程,消去y得到关于x的一元二次方程,根据韦达定理得到两横坐标之和的关于m的关系式,再根据MN的中点在x+y=0上得到两横坐标之和等于-1,列出关于m的方程,求出方程的解得到m的值,把k的值和m的值代入不等式组,在数轴上画出相应的平面区域,求出面积即可.
解答: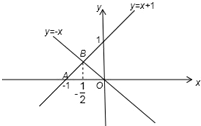 解:因为M与N关于x+y=0对称,
解:因为M与N关于x+y=0对称,
直线y=kx+1与直线x+y=0垂直得到k=1,
所以直线MN的方程为y=x+1;
设M(x1,y1),N(x2,y2),
联立直线与圆的方程得
,
消去y得2x2+(3+m)x+m-3=0则x1+x2=-
;
由MN中点在直线x+y=0上,代入得
+
=0即x1+x2+y1+y2=0,
又MN的中点在y=x+1上,得y1=x1+1,y2=x2+1,所以x1+x2=-1,
则-
=-1,解得m=-1;
所以把k=1,m=-1代入不等式组得
,
画出不等式所表示的平面区域如图
△AOB为不等式所表示的平面区域,联立
解得B(-
,
),A(-1,0),
所以S△AOB=
×|-1|×|-
|=
.
故选A
 解:因为M与N关于x+y=0对称,
解:因为M与N关于x+y=0对称,直线y=kx+1与直线x+y=0垂直得到k=1,
所以直线MN的方程为y=x+1;
设M(x1,y1),N(x2,y2),
联立直线与圆的方程得
|
消去y得2x2+(3+m)x+m-3=0则x1+x2=-
| m+3 |
| 2 |
由MN中点在直线x+y=0上,代入得
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
又MN的中点在y=x+1上,得y1=x1+1,y2=x2+1,所以x1+x2=-1,
则-
| m+3 |
| 2 |
所以把k=1,m=-1代入不等式组得
|
画出不等式所表示的平面区域如图
△AOB为不等式所表示的平面区域,联立
|
| 1 |
| 2 |
| 1 |
| 2 |
所以S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故选A
点评:此题考查学生掌握直线与圆的位置关系,灵活运用韦达定理及中点坐标公式化简求值,会进行简单的线性规划,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目