题目内容
设函数 .
.
(1)若 时,求
时,求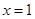 处的切线方程;
处的切线方程;
(2)当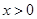 时,
时, ,求
,求 的取值范围.
的取值范围.
(1)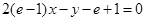 ;(2)
;(2)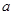 的取值范围是
的取值范围是 .
.
解析试题分析:本题考查函数与导数及运用导数求单调区间、最值等数学知识和方法,突出考查综合运用数学知识和方法分析问题解决问题的能力.第一问,将 代入得到
代入得到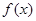 解析式,对
解析式,对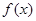 求导,将
求导,将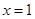 代入得到切线的斜率,再将
代入得到切线的斜率,再将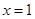 代入
代入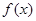 中得到切点的纵坐标,最后利用点斜式方程直接写出切线方程;第二问,将恒成立问题转化成函数
中得到切点的纵坐标,最后利用点斜式方程直接写出切线方程;第二问,将恒成立问题转化成函数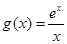 的最小值问题,对
的最小值问题,对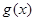 求导,判断
求导,判断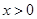 范围内的函数的单调性,判断出当
范围内的函数的单调性,判断出当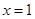 时,
时,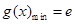 ,所以
,所以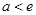 .
.
试题解析:(1)当 ,
,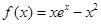
 ,
,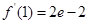 ,
,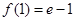 ,
,
故所求切线方程为: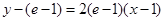 ,
,
化简得: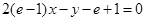 .(5分)
.(5分)
(2) 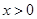 ,
,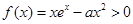 ,
,
化简得: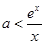 ,
,
设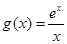 ,
,
求导得: .
.
当 时,
时,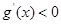 ;当
;当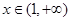 时,
时, .
.
故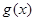 在
在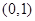 单调减少,在
单调减少,在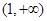 单调增加.
单调增加.
故 在
在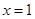 时取极小值.
时取极小值.
则 在
在 时,
时,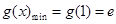 .
.
综上所述: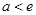 ,即
,即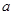 的取值范围是
的取值范围是 .(13分)
.(13分)
考点:1.利用导数求切线方程;2.利用导数判断函数的单调性;3.利用导数求函数最值.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目

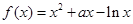 ,
, ;
; 时,求函数
时,求函数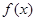 的单调区间;
的单调区间;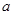 的取值范围;
的取值范围;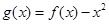 ,是否存在实数
,是否存在实数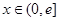 (
(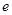 是自然对数的底数)时,函数
是自然对数的底数)时,函数 的最小值是
的最小值是 .若存在,求出
.若存在,求出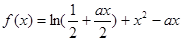
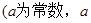 >0)
>0) 的一个极值点,求
的一个极值点,求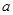 的值;
的值;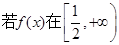 上是增函数,求a的取值范围
上是增函数,求a的取值范围 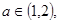 总存在
总存在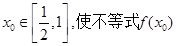 >
>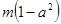 成立,求实数m的取值范围
成立,求实数m的取值范围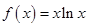 .
.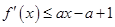 恒成立,求实数a的集合.
恒成立,求实数a的集合.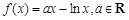 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;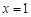 处有极值,求
处有极值,求 ,使
,使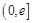 的最小值是3,若存在,求出
的最小值是3,若存在,求出
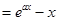 ,其中
,其中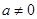 .
.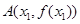 ,
,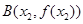
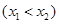 ,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率 为k,问:是否存在x0∈(x1,x2),使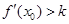 成立?若存在,求
成立?若存在,求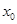 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.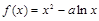 (
(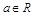 )。
)。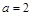 ,求证:
,求证: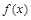 在
在 上是增函数;
上是增函数;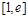 上的最小值。
上的最小值。
 .
.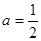 时,求
时,求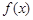 的单调区间;
的单调区间; 在
在 单调递减,求实数
单调递减,求实数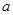 的取值范围.
的取值范围.