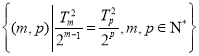题目内容
【题目】已知数列{an}的前n项和为Sn,a1=1,Sn=an+1.
(1)求数列{an}的通项公式;
(2)若![]() ,求数列{bn}的前n项和为Tn.
,求数列{bn}的前n项和为Tn.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)根据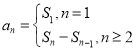 求出数列的通项公式,
求出数列的通项公式,
(2)利用错位相减法即可求出数列{bn}的前n项和为Tn.
(1),a1=1,Sn=an+1=Sn+1﹣Sn,
∴Sn+1=2Sn,
∴数列{Sn}是以1为首项,以2为公比的等比数列,
∴Sn=1×2n﹣1=2n﹣1,
∴an=Sn﹣Sn﹣1=2n﹣2,n≥2,
∴an![]() ,
,
(2)![]() n(
n(![]() )n﹣1,
)n﹣1,
∴Tn=(![]() )0+2(
)0+2(![]() )1+3(
)1+3(![]() )2+…+n(
)2+…+n(![]() )n﹣1,①,
)n﹣1,①,
由①![]() 可得,
可得,
![]() Tn=(
Tn=(![]() )1+2(
)1+2(![]() )2+3(
)2+3(![]() )3+…+n(
)3+…+n(![]() )n,②,
)n,②,
由①﹣②可得![]() Tn=1+(
Tn=1+(![]() )1+(
)1+(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n﹣1﹣n(
)n﹣1﹣n(![]() )n
)n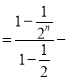 n(
n(![]() )n=2﹣2×(
)n=2﹣2×(![]() )n﹣n(
)n﹣n(![]() )n=2﹣(n+2)(
)n=2﹣(n+2)(![]() )n,
)n,
∴Tn=4![]() .
.

【题目】某生物研究所为研发一种新疫苗,在200只小白鼠身上进行科研对比实验,得到如下统计数据:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 30 |
|
|
注射疫苗 | 70 |
|
|
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(Ⅰ)能否有![]() 的把握认为注射此种疫苗有效?
的把握认为注射此种疫苗有效?
(Ⅱ)在未注射疫苗且未感染病毒与注射疫苗且感染病毒的小白鼠中,分别抽取3只进行病例分析,然后从这6只小白鼠中随机抽取2只对注射疫苗情况进行核实,求抽到的2只均是注射疫苗且感染病毒的小白鼠的概率.
附: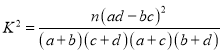 ,
,![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各20次连续正常运行的时间长度(单位:天)数据,并绘制了如下茎叶图:
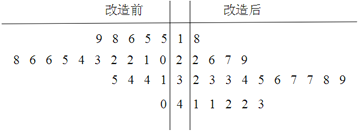
(Ⅰ)(1)设所采集的40个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
试写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根据(1)中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: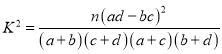 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工厂的生产线的运行需要进行维护.工厂对生产线的生产维护费用包括正常维护费、保障维护费两种对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天(
天(![]() )进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元
)进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元![]() 次;保障维护费第一次为0.2万元
次;保障维护费第一次为0.2万元![]() 周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:
周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:![]() ,
,![]() ,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.