题目内容
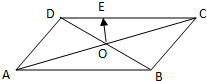如图平行四边形ABCD中，AC，BD相交于O，点E为靠近D的DC的三等分点，设| AB |
| a |
| AD |
| b |
| a |
| b |
| OE |
分析：由已知中平行四边形ABCD中，AC，BD相交于O，且
=
，
=
，利用向量加（减）法的三角形法则，我们可将向量
，
均用
，
表示，又由E为靠近D的DC的三等分点，则
=
+
，整理可得答案．
| AB |
| a |
| AD |
| b |
| OD |
| OC |
| a |
| b |
| OE |
| 2 |
| 3 |
| OD |
| 1 |
| 3 |
| OC |
解答：解：∵平行四边形ABCD中，AC，BD相交于O
则O即为AC的中点，也是BD的中点
故
=
=
（
-
）=
（
-
）
=
=
（
+
）=
（
+
）
又∵E为靠近D的DC的三等分点，
∴
=
+
=
（
-
）+
（
+
）=-
+
故选B
则O即为AC的中点，也是BD的中点
故
| OD |
| 1 |
| 2 |
| BD |
| 1 |
| 2 |
| AD |
| AB |
| 1 |
| 2 |
| b |
| a |
| OC |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AD |
| AB |
| 1 |
| 2 |
| b |
| a |
又∵E为靠近D的DC的三等分点，
∴
| OE |
| 2 |
| 3 |
| OD |
| 1 |
| 3 |
| OC |
| 1 |
| 3 |
| b |
| a |
| 1 |
| 6 |
| b |
| a |
| 1 |
| 6 |
| a |
| 1 |
| 2 |
| b |
故选B
点评：本题考查的知识点是平面向量的基本定理，向量加（减）法的三角形法则，其中将向量
，
均用
，
表示，是解答本题的关键．
| OD |
| OC |
| a |
| b |
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
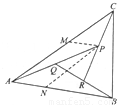
如图，在△ABC中，设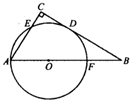
（2012•大连二模）任选一题作答选修：几何证明选讲如图，在△ABC中，∠C=90°，以AB上一点O为圆心，OA长为半径的圆与BC相切于点D，分别交AC、AB于点E、F．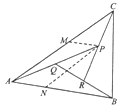
，
，AP的中点为Q，BQ的中点为R，CR的中点恰为P．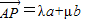
，求λ和μ的值；
．
，
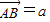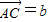，AP的中点为Q，BQ的中点为R，CR的中点恰为P．
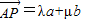，求λ和μ的值；
．