题目内容
等差数列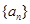 的公差
的公差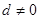 ,
,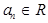 ,前
,前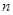 项和为
项和为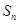 ,则对正整数
,则对正整数 ,下列四个结论中:
,下列四个结论中:
(1)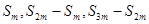 成等差数列,也可能成等比数列;
成等差数列,也可能成等比数列;
(2)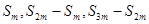 成等差数列,但不可能成等比数列;
成等差数列,但不可能成等比数列;
(3)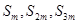 可能成等比数列,但不可能成等差数列;
可能成等比数列,但不可能成等差数列;
(4)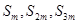 不可能成等比数列,也不可能成等差数列;
不可能成等比数列,也不可能成等差数列;
正确的是( )
| A.(1)(3). | B.(1)(4). | C.(2)(3). | D.(2)(4). |
D
解析试题分析:根据等差数列的性质, ,
,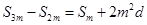 ,
,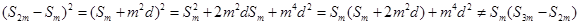 ,因此(1)错误,(2)正确,由上显然有
,因此(1)错误,(2)正确,由上显然有 ,
,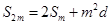 ,
, ,
,
 ,故(3)错误,(4)正确.即填 (2)(4).
,故(3)错误,(4)正确.即填 (2)(4).
考点:等差数列的前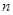 项和,等差数列与等比数列的定义.
项和,等差数列与等比数列的定义.

练习册系列答案
相关题目
在各项均为正数的等比数列 中,公比
中,公比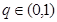 .若
.若 ,
, 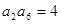 ,
, 数列
数列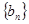 的前
的前 项和为
项和为 ,则当
,则当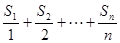 取最大值时,
取最大值时, 的值为( )
的值为( )
| A.8 | B.9 | C.8或9 | D.17 |
已知正数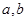 满足:三数
满足:三数 的倒数成等差数列,则
的倒数成等差数列,则 的最小值为( )
的最小值为( )
| A.1 | B.2 | C. | D.4 |
已知等差数列{an}中,|a3|=|a9|,公差d<0,Sn是数列{an}的前n项和,则( )
| A.S5>S6 | B.S5<S6 |
| C.S6=0 | D.S5=S6 |
设Sn为等差数列{an}的前n项和,S8=4a3,a7=-2,则
a9= ( ).
| A.-6 | B.-4 |
| C.-2 | D.2 |
若-9,a,-1成等差数列,-9,m,b,n,-1成等比数列,则ab=( ).
| A.15 | B.-15 | C.±15 | D.10 |
已知等比数列{an}的公比为q,记bn=am(n-1)+1+am(n-1)+2+…+am(n-1)+m,cn=am(n-1)+1·am(n-1)+2·…·am(n-1)+m(m,n∈N*),则以下结论一定正确的是( ).
| A.数列{bn}为等差数列,公差为qm |
| B.数列{bn}为等比数列,公比为q2m |
| C.数列{cn}为等比数列,公比为qm2 |
| D.数列{cn}为等比数列,公比为qmn |
设等差数列{an}的前n项和为Sn,若S3=9,S6=36,则a7+a8+a9=( ).
| A.63 | B.45 | C.36 | D.27 |

