题目内容
设双曲线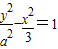 的两个焦点分别为F1、F2,离心率为2.
的两个焦点分别为F1、F2,离心率为2.(Ⅰ)求此双曲线的渐近线l1、l2的方程;
(Ⅱ)若A、B分别为l1、l2上的点,且2|AB|=5|F1F2|,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线.
【答案】分析:(Ⅰ)利用离心率为2,结合c2=a2+3,可求a,c的值,从而可求双曲线方程,即可求得渐近线方程;
(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y),利用2|AB|=5|F1F2|,建立方程,根据A、B分别为l1、l2上的点,化简可得轨迹方程及对应的曲线.
解答:解:(Ⅰ)∵e=2,∴c2=4a2
∵c2=a2+3,∴a=1,c=2
∴双曲线方程为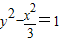 ,渐近线方程为
,渐近线方程为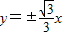
(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y)
∵2|AB|=5|F1F2|,∴|AB|= |F1F2|=
|F1F2|= ×2c=10,∴
×2c=10,∴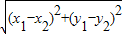 =10
=10
∵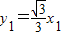 ,
,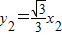 ,2x=x1+x2,2y=y1+y2
,2x=x1+x2,2y=y1+y2
∴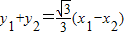 ,
,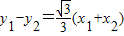
∴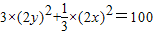
∴ ,对应的曲线为椭圆.
,对应的曲线为椭圆.
点评:本题考查轨迹方程的求解,考查双曲线的几何性质,考查学生的计算能力,属于中档题.
(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y),利用2|AB|=5|F1F2|,建立方程,根据A、B分别为l1、l2上的点,化简可得轨迹方程及对应的曲线.
解答:解:(Ⅰ)∵e=2,∴c2=4a2
∵c2=a2+3,∴a=1,c=2
∴双曲线方程为
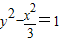 ,渐近线方程为
,渐近线方程为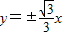
(Ⅱ)设A(x1,y1),B(x2,y2),AB的中点M(x,y)
∵2|AB|=5|F1F2|,∴|AB|=
 |F1F2|=
|F1F2|= ×2c=10,∴
×2c=10,∴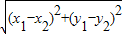 =10
=10∵
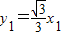 ,
,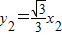 ,2x=x1+x2,2y=y1+y2
,2x=x1+x2,2y=y1+y2∴
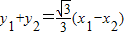 ,
,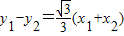
∴
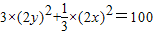
∴
 ,对应的曲线为椭圆.
,对应的曲线为椭圆.点评:本题考查轨迹方程的求解,考查双曲线的几何性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 的两个焦点分别为
的两个焦点分别为 ,离心率为2.
,离心率为2. 的方程;
的方程; 、
、 分别为
分别为 ,求线段
,求线段 的中点
的中点 的轨迹方程,并说明轨迹是什么曲线;
的轨迹方程,并说明轨迹是什么曲线; 分别是双曲线
分别是双曲线 的两个焦点,P是该双曲线上的一点,且
的两个焦点,P是该双曲线上的一点,且 ,则
,则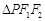 的面积等于
的面积等于 (B)
(B) (C)
(C) (D)
(D)
 分别是双曲线
分别是双曲线 的两个焦点,P是该双曲线上的一点,且
的两个焦点,P是该双曲线上的一点,且 ,则
,则 的面积等于
的面积等于 (B)
(B) (C)
(C) (D)
(D)
 ,且经过点
,且经过点 ,设
,设 是双曲线的两个焦点,点
是双曲线的两个焦点,点 在双曲线上,且
在双曲线上,且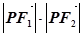 =64.
=64. .
.