题目内容
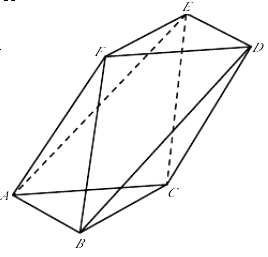
【题目】如图,在以A,B,C,D,E,F为顶点的多面体中,四边形ACDF是菱形,∠FAC=60°,AB∥DE,BC∥EF,AB=BC=3,AF=2 ![]() .
. 
(1)求证:平面ABC⊥平面ACDF;
(2)求平面AEF与平面ACE所成的锐二面角的余弦值.
【答案】
(1)证明:设O是AC中点,连结OF、OB、FC,
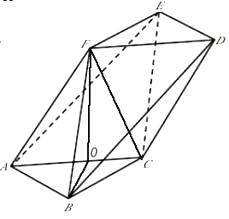
在△ABC中,AB=BC,∴OB⊥AC,
∵四边形ACDF是菱形,∠FAC=60°,
∴△FAC是等边三角形,∴OF⊥AC,
∴∠FOB是二面角F﹣AC﹣B的平面角,
在Rt△FAO中,AF=2 ![]() ,AO=
,AO= ![]() AC=
AC= ![]() AF=
AF= ![]() ,
,
∴OF= ![]() =
= ![]() ,
,
又∵BF= ![]() ,∴OF2+OB2=BF2,
,∴OF2+OB2=BF2,
∴∠FOB=90°,
∴平面ABC⊥平面ACDF.
(2)解:由(1)知OB、OC、OF两两垂直,以O为原点,OB为x轴,OC为y轴,OF为z轴,
建立空间直角坐标系,
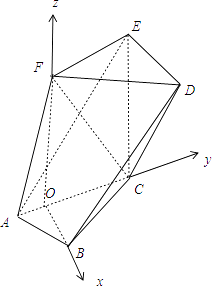
则A(0,﹣ ![]() ,0),B(
,0),B( ![]() ,0,0),C(0,
,0,0),C(0, ![]() ,0),F(0,0,3),
,0),F(0,0,3),
![]() =(0,
=(0, ![]() ,3),
,3), ![]() =(0,2
=(0,2 ![]() ,0),
,0),
∵AB∥DE,AF∥CD,又AB平面CDE,AF平面CDE,
DE平面CDE,CD平面CDE,
∴AB∥平面CDE,AF∥平面CDE,
又AB∩AF=A,∴平面ABF∥平面CDE,
∵EF∥BC,∴B、C、E、F四点共面,
又平面ABF∩平面BCEF=BF,平面CDE∩平面BCEF=CE,
∴BF∥CE,∴四边形BCEF是平行四边形,
∴ ![]() =
= ![]() =(﹣
=(﹣ ![]() ,0),
,0),
∴ ![]() =(﹣
=(﹣ ![]() ,3),
,3),
设平面AEF的法向量 ![]() =(x,y,z),
=(x,y,z),
则 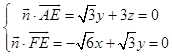 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
设平面ACE的法向量 ![]() =(a,b,c),
=(a,b,c),
则 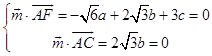 ,取a=
,取a= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
设平面AEF与平面ACE所成的锐二面角为θ,
则cosθ= ![]() =
= ![]() .
.
∴平面AEF与平面ACE所成的锐二面角的余弦值为 ![]() .
.
【解析】(1)设O是AC中点,连结OF、OB、FC,推导出OB⊥AC,OF⊥AC,则∠FOB是二面角F﹣AC﹣B的平面角,由此能证明平面ABC⊥平面ACDF.(2)以O为原点,OB为x轴,OC为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出平面AEF与平面ACE所成的锐二面角的余弦值.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.