题目内容
直线A.1个
B.2个
C.3个
D.4个
解析:设P1(4cosα,3sinα),α∈(0,![]() ),则?
),则?
SP1AOB=S△OAP1+S△OBP1?
=12×4sinα+12×3×4cosα?
=6(sinα+cosα)=6![]() sin(α+
sin(α+![]() ).?
).?
当α=![]() 时,SP1AOB的最大值为6
时,SP1AOB的最大值为6![]() .?
.?
故S△P1AB≤6![]() -S△OAB=6
-S△OAB=6![]() -6<3.?
-6<3.?
故AB的上方不存在满足题意的点P.又S△OAB=6>3,所以AB的下方存在2个点满足要求.
答案:B

练习册系列答案
相关题目
 =0,椭圆C:
=0,椭圆C: +y2=1,F1、F2分别为椭圆C的左、右焦点.
+y2=1,F1、F2分别为椭圆C的左、右焦点. +
+ =1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为
=1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为 .
.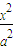 +
+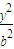 =1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为
=1的焦点为F1(0,3),M(x,4)(x>0)椭圆C上一点,△MOF1的面积为 .
.