题目内容
设函数
．（1）试判定函数f（x）的单调性，并说明理由；
（2）已知函数f（x）的图象在点A（x，f（x））处的切线斜率为
，求
的值．
【答案】分析：（1）求出函数的导函数，利用导数求出函数的单调性区间即可，本题由于导数恒正，故可确定函数是R上是增函数．
（2）令导数等于2，求出切点的横坐标，代入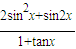
利用三角恒等变换公式化简求值即可．
解答：解：
，
∴f（x）定义域内单调递增．（4分）
（2）由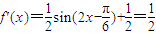
，
得：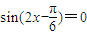
．∴
，
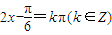得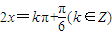
，（4分）
∴
=
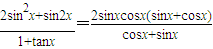
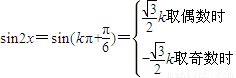（6分）
点评：本题考查正弦函数的单调性及求导公式，解题的关键是正确求出函数的导数，利用导数的意义研究函数的单调性求切点的坐标，本题中二的求值过程中要利用三角恒等式进行化简，三角恒等式由于公式比较多，记忆较难，导致公式记不准或者用不准出错，学习时要善加记忆，多多关注．
（2）令导数等于2，求出切点的横坐标，代入
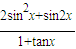利用三角恒等变换公式化简求值即可．解答：解：
，∴f（x）定义域内单调递增．（4分）
（2）由
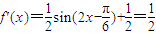，得：
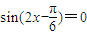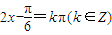．∴，得
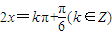，（4分）∴
=
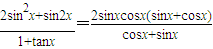
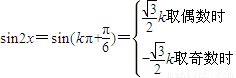（6分）点评：本题考查正弦函数的单调性及求导公式，解题的关键是正确求出函数的导数，利用导数的意义研究函数的单调性求切点的坐标，本题中二的求值过程中要利用三角恒等式进行化简，三角恒等式由于公式比较多，记忆较难，导致公式记不准或者用不准出错，学习时要善加记忆，多多关注．
练习册系列答案
相关题目
。
的单调性，并说明理由；
处的切线斜率为
，求
的值．