题目内容
已知函数f(x)满足f(x)+f'(0)-e-x=-1,函数g(x)=-λlnf(x)+sinx是区间[-1,1]上的减函数.
(1)当x≥0时,曲线y=f(x)在点M(t,f(t))的切线与x轴、y轴围成的三角形面积为S(t),求S(t)的最大值;
(2)若g(x)<t2+λt+1在x∈[-1,1]时恒成立,求t的取值范围;
(3)设函数h(x)=-lnf(x)-ln(x+m),常数m∈Z,且m>1,试判定函数h(x)在区间[e-m-m,e2m-m]内的零点个数,并作出证明.
解:(1)因为f'(x)=(e-x)'=-e-x,f'(0)=-1,切线的斜率为-e-t,切点(t,e-t)
故切线的方程为y-e-t=-e-t(x-t),即e-tx+y-e-t(t+1)=0,…(1分)
令y=0得x=t+1,又令x=0得y=e-t(t+1)
所以
从而 .
.
∵当t∈(0,1)时,S'(t)>0,当t∈(1,+∞)时,S'(t)<0,
所以S(t)的最大值为
(2)由①知:f(x)=e-x,∴g(x)=λx+sinx,
∴g'(x)=λ+cosx,
∵函数g(x)=-λlnf(x)+sinx是区间[-1,1]上的减函数
∴g'(x)=λ+cosx≤0在[-1,1]上恒成立,
∴λ≤-1,g(x)max=-λ-sin1,
∵g(x)<t2+λt+1在x∈[-1,1]时恒成立,
∴-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立,
∴(t+1)λ+t2+sin1+1>0在λ∈(-∞,-1]上恒成立.
令h(λ)=(t+1)λ+t2+sin1+1(λ≤-1),
则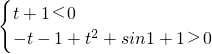 ,∴
,∴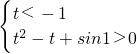 ,
,
而t<-1时,t2-t+sin1>0恒成立,
经检验t=-1也对,∴t≤-1
(3)函数h(x)=x-ln(x+m),x∈(-m,+∞)连续,且
令h′(x)=0,可得x=1-m
当x∈(-m,1-m)时,h'(x)<0,h(x)为减函数,h(x)>h(1-m)
当x∈(1-m,+∞)时,h'(x)>0,h(x)为增函数,h(x)>h(1-m)
根据函数极值判别方法,h(1-m)=1-m为极小值,而且对x∈(-m,+∞)都有h(x)≥h(1-m)=1-m
故当整数m≤1时,h(x)≥1-m≥0
所以当整数m>1时,h(x)存在最小值h(1-m)=1-m<0,函数h(x)=x-ln(x+m)在[e-m-m,e2m-m]上为连续减函数.
因为h(e-m-m)=e-m-m-ln(e-m-m+m)=e-m>0,当整数m>1时,h(e-m-m)与h(1-m)异号
所以存在唯一的x1∈(e-m-m,1-m),使h(x1)=0
而当整数m>1时,h(e2m-m)=e2m-3m>(1+1)2m-3m>1+2m+ -3m>0与h(1-m)异号
-3m>0与h(1-m)异号
所以存在唯一的x2∈(1-m,e2m-m),使h(x2)=0
故当m>1时,方程h(x)=0在[e-m-m,e2m-m]内有两个实根 …(15分)
分析:(1)求切线的斜率,确定切线的方程,进而可表示三角形面积S(t),利用导数的方法,可求S(t)的最大值;
(2)由于g(x)<t2+λt+1在x∈[-1,1]上恒成立,转化为[g(x)]max=g(-1)=-λ-sinl,解出即可;
(3)求导数,确定函数的单调性,从而可得函数的极小值,而且对x∈(-m,+∞)都有h(x)≥h(1-m)=1-m,当整数m≤1时,h(x)≥1-m≥0;当整数m>1时,h(x)存在最小值h(1-m)=1-m<0,再分别确定端点的函数值为正,即可求得函数零点的个数.
点评:本题考查导数知识的运用,考查导数的几何意义,考查恒成立问题,考查函数的零点,考查学生的计算能力,综合性强.
故切线的方程为y-e-t=-e-t(x-t),即e-tx+y-e-t(t+1)=0,…(1分)
令y=0得x=t+1,又令x=0得y=e-t(t+1)
所以

从而
 .
.∵当t∈(0,1)时,S'(t)>0,当t∈(1,+∞)时,S'(t)<0,
所以S(t)的最大值为

(2)由①知:f(x)=e-x,∴g(x)=λx+sinx,
∴g'(x)=λ+cosx,
∵函数g(x)=-λlnf(x)+sinx是区间[-1,1]上的减函数
∴g'(x)=λ+cosx≤0在[-1,1]上恒成立,
∴λ≤-1,g(x)max=-λ-sin1,
∵g(x)<t2+λt+1在x∈[-1,1]时恒成立,
∴-λ-sin1<t2+λt+1在λ∈(-∞,-1]上恒成立,
∴(t+1)λ+t2+sin1+1>0在λ∈(-∞,-1]上恒成立.
令h(λ)=(t+1)λ+t2+sin1+1(λ≤-1),
则
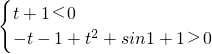 ,∴
,∴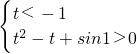 ,
,而t<-1时,t2-t+sin1>0恒成立,
经检验t=-1也对,∴t≤-1
(3)函数h(x)=x-ln(x+m),x∈(-m,+∞)连续,且

令h′(x)=0,可得x=1-m
当x∈(-m,1-m)时,h'(x)<0,h(x)为减函数,h(x)>h(1-m)
当x∈(1-m,+∞)时,h'(x)>0,h(x)为增函数,h(x)>h(1-m)
根据函数极值判别方法,h(1-m)=1-m为极小值,而且对x∈(-m,+∞)都有h(x)≥h(1-m)=1-m
故当整数m≤1时,h(x)≥1-m≥0
所以当整数m>1时,h(x)存在最小值h(1-m)=1-m<0,函数h(x)=x-ln(x+m)在[e-m-m,e2m-m]上为连续减函数.
因为h(e-m-m)=e-m-m-ln(e-m-m+m)=e-m>0,当整数m>1时,h(e-m-m)与h(1-m)异号
所以存在唯一的x1∈(e-m-m,1-m),使h(x1)=0
而当整数m>1时,h(e2m-m)=e2m-3m>(1+1)2m-3m>1+2m+
 -3m>0与h(1-m)异号
-3m>0与h(1-m)异号所以存在唯一的x2∈(1-m,e2m-m),使h(x2)=0
故当m>1时,方程h(x)=0在[e-m-m,e2m-m]内有两个实根 …(15分)
分析:(1)求切线的斜率,确定切线的方程,进而可表示三角形面积S(t),利用导数的方法,可求S(t)的最大值;
(2)由于g(x)<t2+λt+1在x∈[-1,1]上恒成立,转化为[g(x)]max=g(-1)=-λ-sinl,解出即可;
(3)求导数,确定函数的单调性,从而可得函数的极小值,而且对x∈(-m,+∞)都有h(x)≥h(1-m)=1-m,当整数m≤1时,h(x)≥1-m≥0;当整数m>1时,h(x)存在最小值h(1-m)=1-m<0,再分别确定端点的函数值为正,即可求得函数零点的个数.
点评:本题考查导数知识的运用,考查导数的几何意义,考查恒成立问题,考查函数的零点,考查学生的计算能力,综合性强.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目