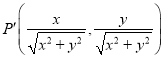题目内容
【题目】椭圆![]() (a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(a>0,b>0)的左右焦点分别为F1,F2,与y轴正半轴交于点B,若△BF1F2为等腰直角三角形,且直线BF1被圆x2+y2=b2所截得的弦长为2,
(1)求椭圆的方程;
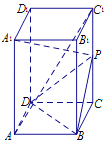
(2)直线l:y=kx+m与椭圆交于点A,C,线段AC的中点为M,射线MO与椭圆交于点P,点O为△PAC的重心,求证:△PAC的面积S为定值;
【答案】(1)![]() 1;(2)见解析
1;(2)见解析
【解析】
(1)由题意得b=c,BF1=2,求出a、b后即可得解;
(2)设A(x1,y1),B(x2,y2),P(x0,y0),联立方程组得![]() ,
,![]() ,由题意x0
,由题意x0![]() ,y0
,y0![]() ,△PAC的面积
,△PAC的面积![]()
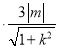 ,化简即可得证.
,化简即可得证.
(1)根据题意,由△BF1F2为等腰直角三角形可得b=c,
直线BF1:y=x+b被圆x2+y2=b2所截得的弦长为2,即BF1=2,
所以a=2,![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() 1;
1;
(2)证明:直线l的方程为y=kx+m,设A(x1,y1),B(x2,y2),
联立![]() ,可得(1+2k2)x2+4kmx+2m2﹣4=0,
,可得(1+2k2)x2+4kmx+2m2﹣4=0,
x1+x2![]() ,x1x2
,x1x2![]() ,y1+y2=k(x1+x2)+2m
,y1+y2=k(x1+x2)+2m![]() ,
,
由题意点O为△PAC重心,设P(x0,y0),可得![]() 0,
0,![]() 0,
0,
所以x0=-(x1+x2)![]() ,y0=-(y1+y2)
,y0=-(y1+y2)![]() ,
,
代入椭圆![]() 1;得
1;得![]() 1,化为2m2=1+2k2,
1,化为2m2=1+2k2,
设坐标原点O到直线l的距离为d,
则△PAC的面积S![]() |AC|3d
|AC|3d![]() |x1﹣x2|
|x1﹣x2|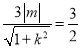 |m||x1﹣x2|
|m||x1﹣x2|![]() |m|
|m|
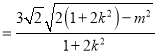 |m|=3
|m|=3![]()
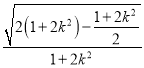
![]() .
.
可得△PAC的面积S为定值![]() .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
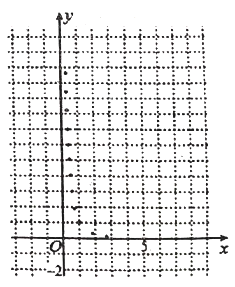
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为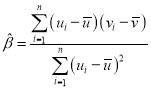 ,
,![]()