题目内容
在棱长为1的正方体中过相邻三个面上的对角线截得一个正三棱锥,则它的高是( )
| A、1 | ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
分析:沿棱长为1的正方体相邻三个面的对角线截去一个棱锥,三条侧棱都是1,求出棱锥的体积,将它的高视为三棱锥的高,利用体积法即可得到选项.
解答: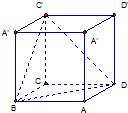 解:沿棱长为1的正方体相邻三个面的对角线截去一个棱锥,如图,
解:沿棱长为1的正方体相邻三个面的对角线截去一个棱锥,如图,
棱锥C′-CBD的体积为:
×
×1×1=
,
又棱锥C-BDC′的体积为:
×
×2×h,
它们是同一个几何体的体积,
∴
×
×2×h=
,
∴h=
,
故选C.
 解:沿棱长为1的正方体相邻三个面的对角线截去一个棱锥,如图,
解:沿棱长为1的正方体相邻三个面的对角线截去一个棱锥,如图,棱锥C′-CBD的体积为:
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
又棱锥C-BDC′的体积为:
| 1 |
| 3 |
| ||
| 4 |
它们是同一个几何体的体积,
∴
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 6 |
∴h=
| ||
| 3 |
故选C.
点评:本题是基础题,考查棱锥的体积,点到平面的距离的求法,多面体的等体积转化,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
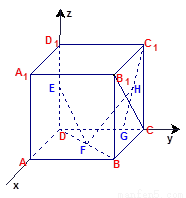
 如图,在棱长为1的正方体中,E是棱A1B1的中点,
如图,在棱长为1的正方体中,E是棱A1B1的中点, 中,若点
中,若点 是棱上一点,则满足
是棱上一点,则满足 的点
的点
 中,
中,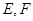 分别是
分别是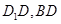 的中点,
的中点,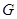 在棱
在棱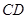 上,且
上,且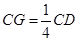 ,H为
,H为 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.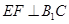 ;
;