题目内容
在棱长为1的正方体中ABCD=A1B1C1D1,M、N分别是AC1、A1B1的中点.点P 在正方体的表面上运动,则总能使MP与BN垂直的点P所构成的轨迹的周长等于 .
分析:取BB1的中点E、CC1的中点F,连接AE、EF、FD,则BN⊥平面AEFD,设M在平面AB1中的射影为O,过MO与平面AEFD平行的平面为α,故能使MP与BN垂直的点P所构成的轨迹为矩形,其周长与矩形AEFD的周长相等.
解答: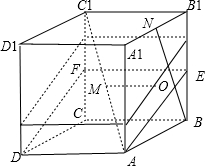 解:取BB1的中点E、CC1的中点F,连接AE、EF、FD,则BN⊥平面AEFD
解:取BB1的中点E、CC1的中点F,连接AE、EF、FD,则BN⊥平面AEFD
设M在平面AB1中的射影为O,过MO与平面AEFD平行的平面为α
∴能使MP与BN垂直的点P所构成的轨迹为矩形,其周长与矩形AEFD的周长相等
∵正方体ABCD=A1B1C1D1的棱长为1
∴矩形AEFD的周长为2+
故答案为:2+
 解:取BB1的中点E、CC1的中点F,连接AE、EF、FD,则BN⊥平面AEFD
解:取BB1的中点E、CC1的中点F,连接AE、EF、FD,则BN⊥平面AEFD设M在平面AB1中的射影为O,过MO与平面AEFD平行的平面为α
∴能使MP与BN垂直的点P所构成的轨迹为矩形,其周长与矩形AEFD的周长相等
∵正方体ABCD=A1B1C1D1的棱长为1
∴矩形AEFD的周长为2+
| 5 |
故答案为:2+
| 5 |
点评:本题考查立体几何中的轨迹问题,考查学生的分析解决问题的能力,解题的关键是确定使MP与BN垂直的点P所构成的轨迹.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在棱长为1的正方体中过相邻三个面上的对角线截得一个正三棱锥,则它的高是( )
| A、1 | ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
 如图,在棱长为1的正方体中,E是棱A1B1的中点,
如图,在棱长为1的正方体中,E是棱A1B1的中点, 中,若点
中,若点 是棱上一点,则满足
是棱上一点,则满足 的点
的点
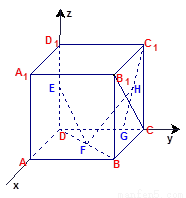
 中,
中,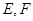 分别是
分别是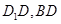 的中点,
的中点,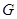 在棱
在棱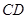 上,且
上,且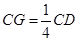 ,H为
,H为 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.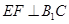 ;
;