题目内容
如图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O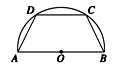
的直径,且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域.
y=-
+2x+4R,定义域为（0，
R）
解析:
AB=2R，C、D在⊙o的半圆周上，
设腰长AD=BC=x，作DE⊥AB，
垂足为E，连接BD，
那么∠ADB是直角，
由此Rt△ADE∽Rt△ABD.
∴AD2=AE×AB，即AE=
，∴CD=AB-2AE=2R-
，
所以y=2R+2x+（2R-
）,即y=-+2x+4R.
再由
,解得0＜x＜
R.所以y=-+2x+4R,定义域为（0，R）.
练习册系列答案
相关题目
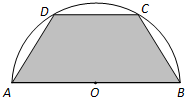如图所示，有一块半径长为1米的半圆形钢板，现要从中截取一个内接等腰梯形部件ABCD，设梯形部件ABCD的面积为y平方米．