题目内容
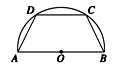
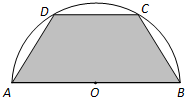 如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.
如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰梯形部件ABCD,设梯形部件ABCD的面积为y平方米.(Ⅰ)按下列要求写出函数关系式:
①设CD=2x(米),将y表示成x的函数关系式;
②设∠BOC=θ(rad),将y表示成θ的函数关系式.
(Ⅱ)求梯形部件ABCD面积y的最大值.
分析:(Ⅰ)以直径AB所在的直线为x轴,线段AB中垂线为y轴,建立平面直角坐标系,过点C作CE垂直于x轴于点E,
①根据题意,利用CD=2x,分别得到梯形的上底,下底和高,再利用梯形的面积公式,列出关于x的函数关系,即可得到答案;
②根据题意,利用∠BOC=θ(rad),分别得到梯形的上底,下底和高,再利用梯形的面积公式,列出关于x的函数关系,即可得到答案;
(Ⅱ)方法1:利用①的表达式,将y=
=
的最大值,转化成t=-x4-2x3+2x+1的最大值,利用导数求出函数的最值,从而确定出y的最大值;
方法2:利用①的表达式,直接对y=(x+1)
进行求导,利用导数即可求得函数的最值;
方法3:利用②的表达式,对y=(1+cosθ)sinθ进行求导,利用导数即可求得函数的最值.
①根据题意,利用CD=2x,分别得到梯形的上底,下底和高,再利用梯形的面积公式,列出关于x的函数关系,即可得到答案;
②根据题意,利用∠BOC=θ(rad),分别得到梯形的上底,下底和高,再利用梯形的面积公式,列出关于x的函数关系,即可得到答案;
(Ⅱ)方法1:利用①的表达式,将y=
| (x+1)2(1-x2) |
| -x4-2x3+2x+1 |
方法2:利用①的表达式,直接对y=(x+1)
| 1-x2 |
方法3:利用②的表达式,对y=(1+cosθ)sinθ进行求导,利用导数即可求得函数的最值.
解答:解:如图所示,以直径AB所在的直线为x轴,线段AB中垂线为y轴,建立平面直角坐标系,过点C作CE垂直于x轴于点E,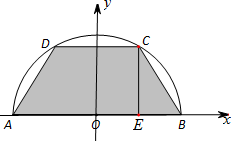
(I)①∵CD=2x,
∴OE=x(0<x<1),CE=
,
∴y=
(|AB|+|CD|)•CE=
(2+2x)
=(x+1)
(0<x<1),
②∵∠BOC=θ(0<θ<
),
∴OE=cosθ,CE=sinθ,
∴y=
(|AB|+|CD|)•CE=
(2+2cosθ)sinθ=(1+cosθ)sinθ(0<θ<
),
(II)(方法1)由①可知,y=(x+1)
,
∴y=
=
,
令t=-x4-2x3+2x+1,
∴t'=-4x3-6x2+2=-2(2x3+3x2-1)=-2(x+1)2(2x-1),
令t'=0,解得x=
,x=-1(舍),
∴当0<x<
时,t'>0,则函数t在(0,
)上单调递增,
当
<x<1时,t'<0,则函数在(
,1)上单调递减,
∴当x=
时,t有最大值
,
∴ymax=
,
答:梯形部份ABCD面积y的最大值为
平方米.
(方法2)由①可知,y=(x+1)
,
∴y′=
+(x+1)×
×
=
,
令y'=0,
∴2x2+x-1=0,(2x-1)(x+1)=0,
∴x=
,x=-1(舍),
∵当0<x<
时,y'>0,则函数y在(0,
)上单调递增,
当
<x<1时,y'<0,则函数y在(
,1)上单调递减,
∴当x=
时,ymax=
,
答:梯形部份ABCD面积的最大值为
平方米.
(方法3)由②可知,
∴y'=[(sinθ+sinθcosθ)]'=(sinθ)'+(sinθ•cosθ)'=cosθ+cos2θ-sin2θ=2cos2θ+cosθ-1,
令y'=0,
∴2cos2θ+cosθ-1=0,解得cosθ=
,即θ=
,cosθ=-1(舍),
∵当0<θ<
时,y'>0,则函数y在(0,
)上单调递增,
当
<θ<
时,y'<0,则函数y在(
,
)上单调递减,
∴当θ=
时,ymax=
,
答:梯形部份ABCD面积的最大值为
平方米.

(I)①∵CD=2x,
∴OE=x(0<x<1),CE=
| 1-x2 |
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1-x2 |
| 1-x2 |
②∵∠BOC=θ(0<θ<
| π |
| 2 |
∴OE=cosθ,CE=sinθ,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
(II)(方法1)由①可知,y=(x+1)
| 1-x2 |
∴y=
| (x+1)2(1-x2) |
| -x4-2x3+2x+1 |
令t=-x4-2x3+2x+1,
∴t'=-4x3-6x2+2=-2(2x3+3x2-1)=-2(x+1)2(2x-1),
令t'=0,解得x=
| 1 |
| 2 |
∴当0<x<
| 1 |
| 2 |
| 1 |
| 2 |
当
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 27 |
| 16 |
∴ymax=
3
| ||
| 4 |
答:梯形部份ABCD面积y的最大值为
3
| ||
| 4 |
(方法2)由①可知,y=(x+1)
| 1-x2 |
∴y′=
| 1-x2 |
| 1 |
| 2 |
| -2x | ||
|
| -2x2-x+1 | ||
|
令y'=0,
∴2x2+x-1=0,(2x-1)(x+1)=0,
∴x=
| 1 |
| 2 |
∵当0<x<
| 1 |
| 2 |
| 1 |
| 2 |
当
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
3
| ||
| 4 |
答:梯形部份ABCD面积的最大值为
3
| ||
| 4 |
(方法3)由②可知,
∴y'=[(sinθ+sinθcosθ)]'=(sinθ)'+(sinθ•cosθ)'=cosθ+cos2θ-sin2θ=2cos2θ+cosθ-1,
令y'=0,
∴2cos2θ+cosθ-1=0,解得cosθ=
| 1 |
| 2 |
| π |
| 3 |
∵当0<θ<
| π |
| 3 |
| π |
| 3 |
当
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴当θ=
| π |
| 3 |
3
| ||
| 4 |
答:梯形部份ABCD面积的最大值为
3
| ||
| 4 |
点评:本题主要考查函数模型的选择与应用,解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.本题以半圆为载体,考查函数模型的构建,关键是腰长表示上底长,考查了利用导数研究函数最值求法以及运算求解的能力,同时考查一题多解,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目