题目内容
(本小题12分)由于高三学习紧张,所以体育、美术两门课开成选修课,高三(1)班共45名学生,最后统计结坚果显示报体育选修的有33人,报美术选修的有36人.假设每个人体育、美术两门课都可以报,并且有5名学生两门都没有报,随机选取该班的1名学生,计算下列事件的概率;
(Ⅰ)他没报了体育选修课;(Ⅱ)他报了美术选修课但是没有报体育选修课;(Ⅲ)他报了体育和美术两门选修课.
解析:
(方法一)(Ⅰ)用A表示事件“他报了体育选修课”,则![]() 就表示事件“他没有报体育选修课”.
就表示事件“他没有报体育选修课”.
因此,选取的人没报体育选修课的概率![]()
(Ⅱ)用B表示事件“他报了美术选修课但是没有报体育选修课”,
C表示事件“他两门选修课都没有报”,
则B和C互斥,并且B+C=![]() . 由P(
. 由P(![]() )=P(B+C)=P(B)+P(C),
)=P(B+C)=P(B)+P(C),
得P(B)=P(![]() )-P(C)=
)-P(C)=![]()
(Ⅲ)用D表示事件“他报了两门选修课”,
E表示事件“他报一门选修课”,则D和B互斥,并且E=D+B.
由P(E)=P(D+B)=P(D)+P(B),得P(D)=P(E)-P(B)=![]()
或设报了两门选修课的人数x,则![]() ∴
∴![]()
(方法二)画出如下韦恩图.
(Ⅰ)他没报了体育选修课: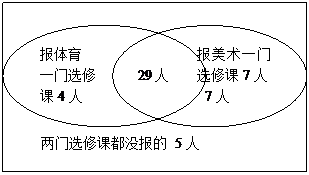
![]()
(Ⅱ)他报了美术选修课但是没有报体育选修课概率
为![]()
(Ⅲ)他喝了1瓶甲饮料和1瓶乙饮料的概率为![]()

练习册系列答案
相关题目

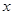 万元,每件产品的成本将降低
万元,每件产品的成本将降低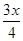 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少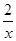 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为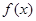 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)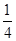 ,不堵车的概率为
,不堵车的概率为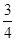 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为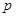 ,不堵车的概率为
,不堵车的概率为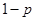 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.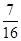 ,求走公路②堵车的概率;
,求走公路②堵车的概率;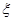 的分布列和数学期望.
的分布列和数学期望.