题目内容
证明在复数范围内,方程|z|2+(1-i)
-(1+i)z=
(i为虚数单位)无解.
| . |
| z |
| 5-5i |
| 2+i |
证明:设这个方程有复数根为z=x+yi(x,y∈R),
则应有x2+y2+(1-i)(x-yi)-(1+i)(x+yi)=
化简得x2+y2-2(x+y)i=1-3i
根据复数相等得
由式(2)得y=
-x
将其代入式(1)得,2x2-3x+
=0(3)
∵△=(-3)2-4×2×
=9-10=-1<0,
∴式(3)无实根,即x不是实数与假设矛盾
所以方程|z|2+(1-i)
-(1+i)z=
没有复数根.
则应有x2+y2+(1-i)(x-yi)-(1+i)(x+yi)=
| 5(1-i)(2-i) |
| 22+12 |
化简得x2+y2-2(x+y)i=1-3i
根据复数相等得
|
由式(2)得y=
| 3 |
| 2 |
将其代入式(1)得,2x2-3x+
| 5 |
| 4 |
∵△=(-3)2-4×2×
| 5 |
| 4 |
∴式(3)无实根,即x不是实数与假设矛盾
所以方程|z|2+(1-i)
| . |
| z |
| 5-5i |
| 2+i |

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
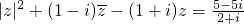 (i为虚数单位)无解.
(i为虚数单位)无解.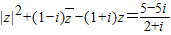 (i为虚数单位)无解.
(i为虚数单位)无解.