题目内容
已知函数y=e|lnx|-|x-1|,则满足f(1-x02)>f(2x0)的x0的取值集合为
{x0|
-1<x0<1}
| 2 |
{x0|
-1<x0<1}
.| 2 |
分析:将函数化为分段函数,然后得到函数在(0,1)上是减函数,在(1,+∞)上是常数1.因此得f(1-x02)>f(2x0)等价于两种情况的并集:1>2x0>1-x02或2x0≥1>1-x02,最后通过讨论得出不等式的解集合.
解答:解:y=e|lnx|-|x-1|=
,
函数在(0,1)上是减函数,在(1,+∞)上是常数1
因此可得,f(1-x02)>f(2x0)等价于
1>2x0>1-x02或2x0≥1>1-x02
(1)由1>2x0>1-x02,得
-1<x0<
;
(2)由2x0≥1>1-x02,得
≤x0<1
综上所述,得x0的取值集合为{x0|
-1<x0<1}
故答案为{x0|
-1<x0<1}
|
函数在(0,1)上是减函数,在(1,+∞)上是常数1
因此可得,f(1-x02)>f(2x0)等价于
1>2x0>1-x02或2x0≥1>1-x02
(1)由1>2x0>1-x02,得
| 2 |
| 1 |
| 2 |
(2)由2x0≥1>1-x02,得
| 1 |
| 2 |
综上所述,得x0的取值集合为{x0|
| 2 |
故答案为{x0|
| 2 |
点评:本题以指数型复合函数为载体,考查了函数与方程的相关知识,属于中档题.解题的关键是将函数化为分段函数的形式,利用函数的单调性与函数的图象相结合.

练习册系列答案
相关题目
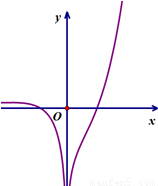
 已知函数y=f(x)的大致图象如图所示,则函数y=f(x)的解析式应为( )
已知函数y=f(x)的大致图象如图所示,则函数y=f(x)的解析式应为( )