题目内容
已知双曲线
解析:设在左支上存在P点,使|PF1|2=|PF2|·d.
由双曲线的第二定义,知?
![]() =
=![]() =e,即|PF2|=e|PF1|.①
=e,即|PF2|=e|PF1|.①
再由双曲线的第一定义,得|PF2|-|PF1|=2a.②?
由①②解得|PF1|=![]() ,|PF2|=
,|PF2|=![]() .?
.?
在△PF1F2中,有|PF1|+|PF2|≥2c,
即![]() +
+![]() ≥2c.③?
≥2c.③?
利用e=![]() ,由③式得e2-2e-1≤0.
,由③式得e2-2e-1≤0.
解得1-2≤e≤1+2.
又由e>1,得1
因此符合条件的点P不存在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




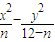 =1的离心率为
=1的离心率为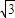 ,则n= .
,则n= .