题目内容
已知双曲线| x2 |
| cos2θ |
| y2 |
| sin2θ |
分析:由题意双曲线
-
=1(θ为锐角)的右焦为F,易有F(1,0),又因为P是右支上任意一点,以P为圆心,PF长为半径的圆在右准线上截得的弦长恰好等于|PF|,所以的到三角形ABP为正三角形,利用离心率的概念得到θ角的方程解出即可.
| x2 |
| cos2θ |
| y2 |
| sin2θ |
解答:解:由题意画一草图分析如下:
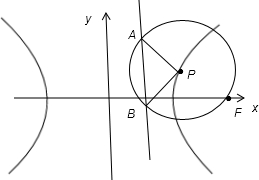
由于双曲线
-
=1(θ为锐角)的右焦为F,易有F(1,0),又因为P是右支上任意一点,以P为圆心,PF长为半径的圆在右准线上截得的弦长恰好等于|PF|,又P为圆心,PF长为半径的圆在右准线上截得的弦长恰好等于|PF|得,P到右准线的距离为半径的
,又P到右焦点的距离为半径,
所以,离心率为
=
(θ∈(0,90°)⇒θ=
.
故答案为:
.

由于双曲线
| x2 |
| cos2θ |
| y2 |
| sin2θ |
| ||
| 2 |
所以,离心率为
| 2 | ||
|
| 1 |
| cosθ |
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:此题考查了双曲线的标准方程已经知道求解焦点坐标,还考查了题意理解及双曲线的离心率的定义及解三角方程.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目