题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,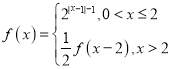 ,则
,则![]() ,在
,在![]() 上所有零点之和为( )
上所有零点之和为( )
A.7 B.8 C.9 D.10
【答案】B
【解析】
试题分析:∵函数f(x)是定义在R上的奇函数,∴f(-x)=-f(x).又∵函数g(x)=xf(x)-1,∴g(-x)=(-x)f(-x)-1=(-x)[-f(x)]-1=xf(x)-1=g(x),∴函数g(x)是偶函数,∴函数g(x)的零点都是以相反数的形式成对出现的.∴函数g(x)在[-6,6]上所有的零点的和为0,∴函数g(x)在[-6,+∞)上所有的零点的和,即函数g(x)在(6,+∞)上所有的零点之和.由0<x≤2时,f(x)=2|x-1|-1,即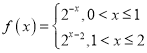 ,∴函数f(x)在(0,2]上的值域为[
,∴函数f(x)在(0,2]上的值域为[![]() ,1],当且仅当x=2时,f(x)=1,又∵当x>2时,f(x)=
,1],当且仅当x=2时,f(x)=1,又∵当x>2时,f(x)=![]() f(x-2),∴函数f(x)在(2,4]上的值域为[
f(x-2),∴函数f(x)在(2,4]上的值域为[![]() ],函数f(x)在(4,6]上的值域为[
],函数f(x)在(4,6]上的值域为[![]() ],函数f(x)在(6,8]上的值域为[
],函数f(x)在(6,8]上的值域为[![]() ],当且仅当x=8时,f(x)=
],当且仅当x=8时,f(x)=![]() ,函数f(x)在(8,10]上的值域为[
,函数f(x)在(8,10]上的值域为[![]() ],当且仅当x=10时,f(x)=
],当且仅当x=10时,f(x)=![]() ,故f(x)<
,故f(x)<![]() 在(8,10]上恒成立,g(x)=xf(x)-1在(8,10]上无零点,同理g(x)=xf(x)-1在(10,12]上无零点,依此类推,函数g(x)在(8,+∞)无零点,综上函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为8,故选B
在(8,10]上恒成立,g(x)=xf(x)-1在(8,10]上无零点,同理g(x)=xf(x)-1在(10,12]上无零点,依此类推,函数g(x)在(8,+∞)无零点,综上函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为8,故选B

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
