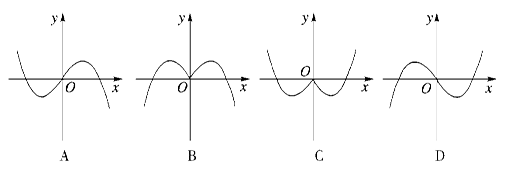
题目内容
若函数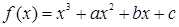 有极值点
有极值点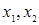 ,且
,且 ,若关于
,若关于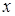 的方程
的方程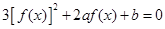 的不同实数根的个数是( )
的不同实数根的个数是( )
| A.3 | B.4 | C.5 | D.6 |
A
解析试题分析: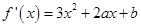 ,因为函数
,因为函数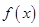 有极值点
有极值点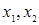 ,则
,则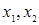 是方程
是方程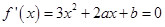 的两根。即
的两根。即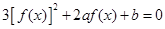 时
时  或
或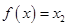 。因为
。因为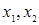 (且
(且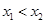 )是方程
)是方程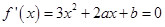 的两根,所以令
的两根,所以令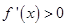 得
得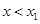 或
或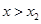 ,令
,令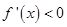 得
得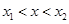 ,所以函数
,所以函数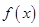 在
在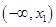 和
和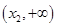 上单调递增,在
上单调递增,在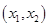 上单调递减。当
上单调递减。当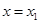 时函数
时函数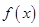 取得极大值为
取得极大值为 ,当
,当 时函数
时函数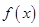 取得极小值为
取得极小值为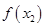 。因为
。因为 由数形结合分析可知所求方程根的个数为3个。
由数形结合分析可知所求方程根的个数为3个。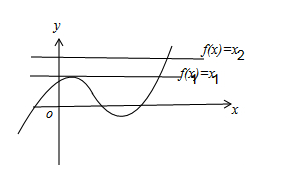
考点:1函数的零点与方程根的关系;2用导数研究函数的性质。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 ,若曲线
,若曲线 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数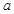 的取值范围是( )
的取值范围是( )
A.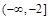 | B. | C.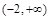 | D.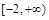 |
函数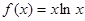 ,则( )
,则( )
A.在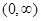 上递增; 上递增; | B.在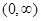 上递减; 上递减; |
C.在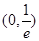 上递增; 上递增; | D.在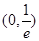 上递减 上递减 |
若函数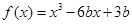 在(0,1)内有极小值,则实数b的取值范围是( )
在(0,1)内有极小值,则实数b的取值范围是( )
| A.(0,1) | B.(0,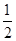 ) ) | C.(0,+∞) | D.(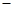 ∞,1) ∞,1) |
设三次函数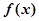 的导函数为
的导函数为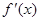 ,函数
,函数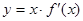 的图象的一部分如下图所示,则( )
的图象的一部分如下图所示,则( )
A.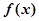 极大值为 极大值为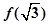 ,极小值为 ,极小值为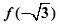 |
B.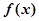 极大值为 极大值为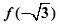 ,极小值为 ,极小值为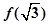 |
C.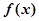 极大值为 极大值为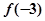 ,极小值为 ,极小值为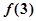 |
D.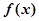 极大值为 极大值为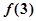 ,极小值为 ,极小值为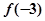 |
设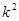 ,若
,若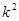 ,则
,则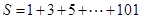 ( )
( )
A.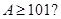 | B.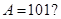 | C.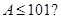 | D.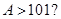 |
函数f(x)=x2-2lnx的单调递减区间是( )
| A.(0,1] | B.[1,+∞) |
| C.(-∞,-1]∪(0,1] | D.[-1,0)∪(0,1] |
若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是( )
| A.[1,+∞) | B.[1,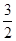 ) ) | C.[1,2) | D.[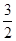 ,2) ,2) |
 的导函数原点处的部分图象大致为 ( )
的导函数原点处的部分图象大致为 ( )