题目内容
9.某三棱锥的三视图如图所示,该三棱锥四个面的面积中最大值是2$\sqrt{34}$.
分析 由题意和三视图知,需要从对应的长方体中确定三棱锥,根据三视图的数据和几何体的垂直关系,求出四面体四个面的面积,再确定出它们的最大值.
解答 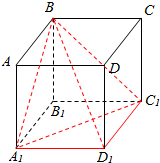 解:将该几何体放入在长方体中,且长、宽、高为4、3、4,
解:将该几何体放入在长方体中,且长、宽、高为4、3、4,
由三视图可知该三棱锥为B-A1D1C1,
由三视图可得,A1D1=CC1=4、D1C1=3,
所以BA1=A1C1=5,BC1=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
则三角形BA1C1的面积S=$\frac{1}{2}$×BC1×h=$\frac{1}{2}$×4$\sqrt{2}$×$\sqrt{{5}^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{34}$,
因为A1D1⊥平面ABA1B1,所以A1D1⊥A1B,
则三角形BA1D1的面积S=$\frac{1}{2}$×BA1×A1D1=$\frac{1}{2}$×4×5=10,
同理可得,三角形BD1C1的面积S=$\frac{1}{2}$×BC1×D1C1=$\frac{1}{2}$×3×4$\sqrt{2}$=6$\sqrt{2}$,
又三角形A1D1C1的面积S=$\frac{1}{2}$×D1C1×A1D1=$\frac{1}{2}$×4×3=6,
所以最大的面为A1BC1,且面积为2$\sqrt{34}$,
故答案为:2$\sqrt{34}$.
点评 本题考查三视图与几何体的直观图的关系,几何体的表面积以及体积的求法,考查计算能力

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+bx+c,(-4≤x<0)}\\{-x+3,(x≥0)}\end{array}\right.$,若f(-4)=f(0),f(-2)=-1.
设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+bx+c,(-4≤x<0)}\\{-x+3,(x≥0)}\end{array}\right.$,若f(-4)=f(0),f(-2)=-1.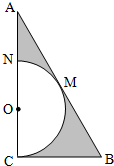 如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.
如图,△ABC中,∠C=90°,∠A=30°,BC=1,在三角形内挖去半圆,圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于点N,则图中阴影部分绕直线AC旋转一周所得旋转体的体积为$\frac{5\sqrt{3}}{27}π$.