题目内容
甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、 “迎迎”和“妮妮各一个”),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止,记游戏终止时投掷骰子的次数为ξ。
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ。
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ。
解:(1)当ξ=7时,甲赢意味着“第七次甲赢,前6次赢5次,但根据规则,前5次中必输1次”,由规则,每次甲赢或乙赢的概率均为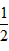 ,因此
,因此 =
=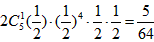 ;
;
(2)设游戏终止时骰子向上的点数是奇数出现的次数为m,向上的点数是偶数出现的次数为n,
则由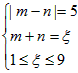 ,
,
可得:当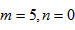 或m=0,n=5时,
或m=0,n=5时,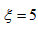 ,
,
当m=6,n=1或m=1,n=6时,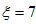 ,
,
当m=7,n=2或m=2,n=7时,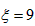 ,
,
因此ξ的可能取值是5、7、9,
每次投掷甲赢得乙一个福娃与乙赢得甲一个福娃的可能性相同,其概率都是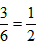 ,
,
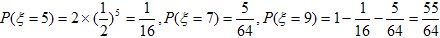
所以ξ的分布列是:
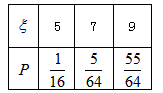
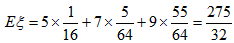 。
。
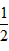 ,因此
,因此 =
=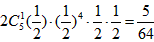 ;
;(2)设游戏终止时骰子向上的点数是奇数出现的次数为m,向上的点数是偶数出现的次数为n,
则由
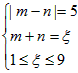 ,
,可得:当
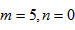 或m=0,n=5时,
或m=0,n=5时,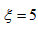 ,
,当m=6,n=1或m=1,n=6时,
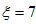 ,
,当m=7,n=2或m=2,n=7时,
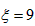 ,
,因此ξ的可能取值是5、7、9,
每次投掷甲赢得乙一个福娃与乙赢得甲一个福娃的可能性相同,其概率都是
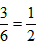 ,
,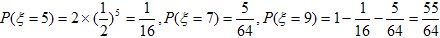
所以ξ的分布列是:

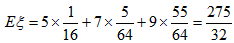 。
。
练习册系列答案
相关题目