题目内容
圆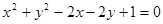 上的点到直线
上的点到直线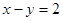 的距离最大值是( )
的距离最大值是( )
| A.2 | B.1+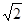 | C.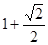 | D.1+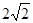 |
B
解析试题分析:因为圆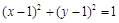 ,而所求距离最大值为圆心到直线距离加半径,即
,而所求距离最大值为圆心到直线距离加半径,即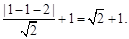
考点:直线与圆位置关系

练习册系列答案
相关题目
已知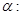 “
“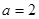 ”;
”;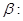 “直线
“直线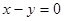 与圆
与圆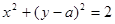 相切”.则
相切”.则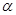 是
是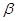 的( )
的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
直线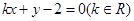 与圆
与圆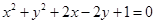 的位置关系是
的位置关系是
| A.相交 | B.相切 | C.相离 | D.与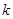 值有关 值有关 |
若圆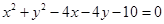 上至少有三个不同点到直线
上至少有三个不同点到直线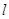 :
: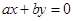 的距离为
的距离为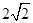 ,则直线
,则直线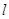 的斜率的取值范围是 ( )
的斜率的取值范围是 ( )
A.[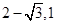 ] ] | B.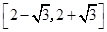 | C.[ | D.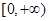 |
如果直线 将圆
将圆 平分且不通过第四象限,则
平分且不通过第四象限,则 的斜率的取值范围是( )
的斜率的取值范围是( )
A. | B. | C. | D. |
[2014·湖北模拟]若直线y=x+b与曲线y=3-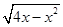 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( )
A.[1-2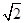 ,1+2 ,1+2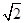 ] ] | B.[1-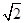 ,3] ,3] |
C.[-1,1+2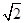 ] ] | D.[1-2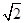 ,3] ,3] |
若圆心在x轴上、半径为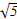 的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是( )
A.(x-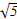 )2+y2=5 )2+y2=5 | B.(x+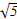 )2+y2=5 )2+y2=5 |
| C.(x-5)2+y2=5 | D.(x+5)2+y2=5 |
若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是( )
| A.2 | B.3 | C.4 | D.6 |
已知圆C经过A(5,2),B(-1,4)两点,圆心在x轴上,则圆C的方程是( )
| A.(x-2)2+y2=13 | B.(x+2)2+y2=17 |
| C.(x+1)2+y2=40 | D.(x-1)2+y2=20 |