题目内容
若圆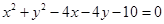 上至少有三个不同点到直线
上至少有三个不同点到直线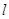 :
: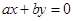 的距离为
的距离为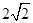 ,则直线
,则直线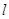 的斜率的取值范围是 ( )
的斜率的取值范围是 ( )
A.[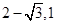 ] ] | B.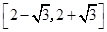 | C.[ | D.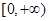 |

解析试题分析:由已知得,圆心为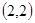 ,半径为
,半径为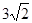 ,根据题意知,只有圆心到直线的距离
,根据题意知,只有圆心到直线的距离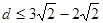 时圆上至少有三个不同点到直线的距离为
时圆上至少有三个不同点到直线的距离为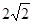 ,即
,即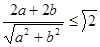 ,所以有
,所以有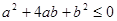 ①,
①,
当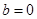 时有
时有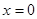 ,此时圆心到直线
,此时圆心到直线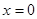 的距离为
的距离为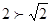 ,不成立;
,不成立;
当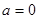 时有
时有 ,此时圆心到直线
,此时圆心到直线 的距离为
的距离为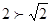 ,不成立;
,不成立;
当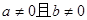 时,直线
时,直线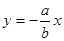 ,则
,则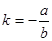 ,将①式同时除以
,将①式同时除以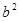 得
得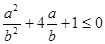 ,
,
即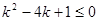 ,解得
,解得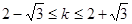 .
.
综上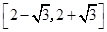 .
.
考点:直线与圆的位置关系的判断.关于直线斜率的讨论.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
过点A(-1,0),斜率为k的直线,被圆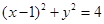 截得的弦长为2
截得的弦长为2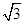 ,则k的值为( )。
,则k的值为( )。
A.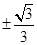 | B. | C.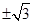 | D.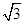 |
设点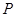 是函数
是函数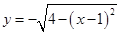 图象上的任意一点,点
图象上的任意一点,点 ,则
,则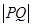 的最小值为( )
的最小值为( )
A.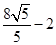 | B. | C.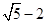 | D.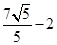 |
直线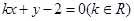 与圆
与圆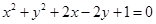 的位置关系是
的位置关系是
| A.相交 | B.相切 | C.相离 | D.与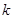 值有关 值有关 |
圆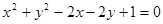 上的点到直线
上的点到直线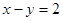 的距离最大值是( )
的距离最大值是( )
| A.2 | B.1+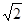 | C.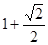 | D.1+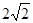 |
直线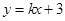 与圆
与圆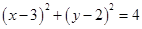 相交于M,N两点,若
相交于M,N两点,若 ,则
,则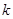 的取值范围是( )
的取值范围是( )
A.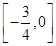 | B.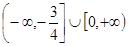 |
C.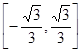 | D.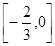 |
直线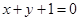 被圆
被圆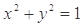 所截得的弦长为( )
所截得的弦长为( )
A.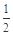 | B.1 | C.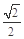 | D.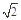 |
若曲线C:x2+y2+2ax-4ay+5a2-4=0上所有的点均在第二象限内,则a的取值范围为( )
| A.(-∞,-2) | B.(-∞,-1) |
| C.(1,+∞) | D.(2,+∞) |
直线x+2y-5+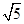 =0被圆x2+y2-2x-4y=0截得的弦长为( ).
=0被圆x2+y2-2x-4y=0截得的弦长为( ).
| A.1 | B.2 |
| C.4 | D.4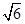 |