题目内容
若（x2-
的展弄式中含x的项为第6项，设（1-3x）n=a+a1x+a2x2+…+anxn，则al+a2+…+an的值为 ．
【答案】分析：利用（x2-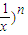
的展开式的通项，结合含x的项为第6项，确定n的值，再利用赋值法确定系数的和．
解答：解：（x2-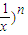
的展开式的通项为
=
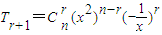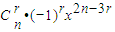
由题意，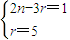
，∴n=8，
∴（1-3x）8=a+a1x+a2x2+…+a8x8，
令x=0，则a=1，令x=1，则a+a1+a2+…+a8=256
∴a1+a2+…+a8=255
故答案为255．
点评：本题考查二项展开式，考查系数和的计算，考查学生的计算能力，属于基础题．
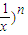的展开式的通项，结合含x的项为第6项，确定n的值，再利用赋值法确定系数的和．解答：解：（x2-
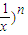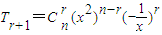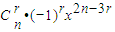
的展开式的通项为=由题意，
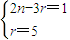，∴n=8，∴（1-3x）8=a+a1x+a2x2+…+a8x8，
令x=0，则a=1，令x=1，则a+a1+a2+…+a8=256
∴a1+a2+…+a8=255
故答案为255．
点评：本题考查二项展开式，考查系数和的计算，考查学生的计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目