题目内容
(本小题满分12分)
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的
菱形,且![]() ,侧棱AA1长等于3a,O为底面ABCD对
,侧棱AA1长等于3a,O为底面ABCD对
角线的交点.
(1)求证:OA1∥平面B1CD1;
(2)求异面直线AC与A1B所成的角;
(3)在棱![]() 上取一点F,问AF为何值时,C1F⊥平面BDF?
上取一点F,问AF为何值时,C1F⊥平面BDF?
(2)![]()
解析:
(方法一)(1) 连A1C1,设其与B1D1交于点O1. ∵A1O1![]() OC, ∴四边形A1O1OC为平行四边形, ∴OA1//O1C,
OC, ∴四边形A1O1OC为平行四边形, ∴OA1//O1C, ![]() 平面B1CD1,
平面B1CD1, ![]() 平面B1CD1, ∴OA1∥平面B1CD1.
平面B1CD1, ∴OA1∥平面B1CD1.
(2) ∵A1C1//AC,∴![]() 就是异面直线AC与A1B所成的角或其补角.
就是异面直线AC与A1B所成的角或其补角.
由题意得![]()
根据余弦定理得 ![]()
故异面直线AC与A1B所成的角为![]()
(3) ∵ABCD是菱形,∴![]() 又
又![]() ∴
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]()
故C1F⊥平面BOF ![]()
![]() ∴
∴![]() .
.
设![]() ,则
,则![]() ∴
∴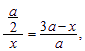 即
即![]()
 解得
解得![]() 故当AF
故当AF![]() 时,C1F⊥平面BOF.
时,C1F⊥平面BOF.
(方法二) 以O为原点,OC、OD所在直线分别为
x轴、y轴,则O(0, 0, 0), ![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
(1) ![]()
![]()
∴![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴OA1∥平面B1CD1.
(2)![]() ,
,![]() ,
,
于是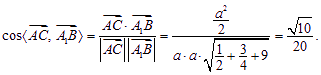
故异面直线AC与A1B所成的角为![]()
(3) 设![]() 为
为![]() 上任意一点,则
上任意一点,则![]() .
.
∵![]() ,于是C1F⊥平面BOF
,于是C1F⊥平面BOF![]()
![]()
解得![]() . 即
. 即![]() 时,C1F⊥平面BOF.
时,C1F⊥平面BOF.

练习册系列答案
相关题目