Question

等比数列{a_n}同时满足下列条件：①a₁+a₆=33,②a₃a₄=32,③三个数4a₂,2a₃,a₄依次成等差数列.

(1)求数列{a_n}的通项公式；

(2)设S_n是数列{a_n}的前n项和，证明＜1;

(3)记b_n=，求数列{b_n}的前n项和T_n.

Answer 1

解析：(1)由得或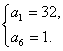

∴a_n=2^n-1或a_n=32·()^n-1，又4a₂,2a₃,a₄依次成等差数列，∴a_n=32·()^n-1舍，所以数列{a_n}的通项公式为a_n=2^n-1

(2)由a_n=2^n-1，得S_n=2ⁿ-1，所以=.

＜=1.所以＜1.

(3)因为b_n==，所以T_n=1+++…+，                 ①

T_n=+++…++,                                            ②

①-②得：T_n=1++++…+-，所以T_N=4(1--).