题目内容
等比数列{an}同时满足下列三个条件:①a1+a6=33;②a2a5=32;③三个数2a2,a32,3a4+4依次成等差数列,求数列{an}的通项公式及前n项和Sn.
【答案】分析:由①②求出a1,a6 的值,求出an=2n-1或an=26-n.再通过③验证,确定通项公式,再根据等比数列前n项和公式计算出Sn.
解答:解:由等比数列性质,a1•a6 =a2a5=32,又a1+a6=33.∴a1,a6是方程x2-33x+32=0的两根,解得①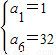 ,此时q=2,通项公式为an=2n-1,三个数2a2,a32,3a4+4依次为:4,16,28,成等差数列,符合题意.
,此时q=2,通项公式为an=2n-1,三个数2a2,a32,3a4+4依次为:4,16,28,成等差数列,符合题意.
或②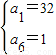 ,此时q=
,此时q= ,通项公式为an=32×
,通项公式为an=32×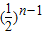 =26-n,三个数2a2,a32,3a4+4依次32,64,16,不成等差数列.
=26-n,三个数2a2,a32,3a4+4依次32,64,16,不成等差数列.
∴数列{an}的通项公式an=2n-1;
∴Sn=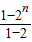 =2n-1.
=2n-1.
点评:本题考查等比数列的性质、通项公式、前n项和Sn.在解题中,应用性质能有效的减少运算量.
解答:解:由等比数列性质,a1•a6 =a2a5=32,又a1+a6=33.∴a1,a6是方程x2-33x+32=0的两根,解得①
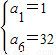 ,此时q=2,通项公式为an=2n-1,三个数2a2,a32,3a4+4依次为:4,16,28,成等差数列,符合题意.
,此时q=2,通项公式为an=2n-1,三个数2a2,a32,3a4+4依次为:4,16,28,成等差数列,符合题意.或②
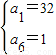 ,此时q=
,此时q= ,通项公式为an=32×
,通项公式为an=32×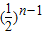 =26-n,三个数2a2,a32,3a4+4依次32,64,16,不成等差数列.
=26-n,三个数2a2,a32,3a4+4依次32,64,16,不成等差数列.∴数列{an}的通项公式an=2n-1;
∴Sn=
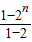 =2n-1.
=2n-1.点评:本题考查等比数列的性质、通项公式、前n项和Sn.在解题中,应用性质能有效的减少运算量.

练习册系列答案
相关题目