题目内容
定义运算：
=ad-bc，若数列{an}满足
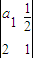=1，且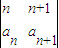
=2（n∈N*）则a3= ．数列{an}的通项公式为an= ．
【答案】分析：由题设知a1=2，nan+1-（n+1）an=2，由此能推出数列的前4项，再观察这前4项，猜想它的通项公式．
解答：解：∵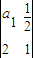
=1，且
=2（n∈N*），
∴a1=2，nan+1-（n+1）an=2，
∴a2-2×2=2，a2=6．
2a3-3×6=2，a3=10．
3a4-4×10=2，a4=14．
∵a1=4×1-2，
a2=4×2-2，
a3=4×3-2，
a4=4×4-2，
由此猜想an=4n-2．
故答案为：10；4n-2．
点评：本题考查数列的性质和应用，解题时要注意公式的合理运用．
解答：解：∵
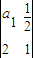=1，且=2（n∈N*），∴a1=2，nan+1-（n+1）an=2，
∴a2-2×2=2，a2=6．
2a3-3×6=2，a3=10．
3a4-4×10=2，a4=14．
∵a1=4×1-2，
a2=4×2-2，
a3=4×3-2，
a4=4×4-2，
由此猜想an=4n-2．
故答案为：10；4n-2．
点评：本题考查数列的性质和应用，解题时要注意公式的合理运用．
练习册系列答案
相关题目
定义运算
=ad-bc，则符合条件
=0的复数z对应的点在（ ）
|
|
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |