题目内容
已知P是三角形ABC内一点,且满足
+
+
=
,则P为三角形ABC的( )
| PA |
| PB |
| PC |
| 0 |
分析:根据题意得到
+
=
,从而以PA、PB为邻边作平行四边形PBDA,由向量的加法法则证出
=
且AB、PD互相平分,得到CP在△ABC的AB边上的中线上,同理P也在BC、AC边上的中线上,由此可得答案.
| PA |
| PB |
| CP |
| CP |
| PD |
解答:解:∵P是三角形ABC内一点,满足
+
+
=
,
∴
+
=-
=
以PA、PB为邻边作平行四边形PBDA,可得
+
=
∴
=
,
∵四边形PBDA的对角线AB、PD互相平分,
∴AB、PD的交点H为AB的中点,得CP在△ABC的AB边上的中线上
同理可得P也在BC、AC边上的中线上,
因此,P为三角形ABC的重心
故选:B
| PA |
| PB |
| PC |
| 0 |

∴
| PA |
| PB |
| PC |
| CP |
以PA、PB为邻边作平行四边形PBDA,可得
| PA |
| PB |
| PD |
∴
| CP |
| PD |
∵四边形PBDA的对角线AB、PD互相平分,
∴AB、PD的交点H为AB的中点,得CP在△ABC的AB边上的中线上
同理可得P也在BC、AC边上的中线上,
因此,P为三角形ABC的重心
故选:B
点评:本题给出三角形内部点P满足的向量式,求P点是三角形的哪一个心.着重考查了三角形的中线的性质、向量的加法法则和向量法解决几何问题等知识,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
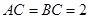 ,
,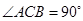 ,
,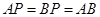 ,
,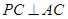 .
.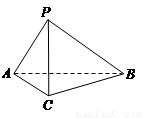
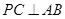 ;
;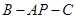 的大小;
的大小;