题目内容

已知P是三角形ABC内一点，若
OP
=
OA
+λ(
AB
|
AB
|cosB
+
AC
|
AC
|cosC
)（λ≠0），则点P应在（　　）
分析：由
OP
=
OA
+λ(
AB
|
AB
|cosB
+
AC
|
AC
|cosC
)，可化为
AP
=λ（
AB
|
AB
|cosB
+
AC
|
AC
|cosC
），两边同乘以向量
BC
，利用向量的数量积运算可求得
AP
•
BC
=0，从而得到结论．
解答：解：
OP
=
OA
+λ(
AB
|
AB
|cosB
+
AC
|
AC
|cosC
)，可化为
AP
=λ（
AB
|
AB
|cosB
+
AC
|
AC
|cosC
），
两边同乘以向量
BC
，得
AP
•
BC
=λ（
AB
|
AB
|cosB
+
AC
|
AC
|cosC
）•
BC

=λ(
AB
•
BC
|
AB
|cosB
+
AC
•
BC
|
AC
|cosC
)=λ（
|
AB
||
BC
|(-cosB)
|
AB
|cosB
+
|
AC
||
BC
|cosC
|
AC
|cosC
）=λ（-|
BC
|+|
BC
|）=0，
所以
AP
⊥
BC
，即点P在在BC边的高线上，
故选C．
点评：本题考查平面向量数量积的运算、向量的线性运算性质及其几何意义，属中档题．
练习册系列答案
相关题目
已知P是三角形ABC内一点，且满足
PA
+
PB
+
PC
=
0
，则P为三角形ABC的（　　）
已知直角三角形ABC的三边a，b，c成公差为正数的等差数列，且a=6．
（1）求三角形ABC的三边长；
（2）设P是三角形ABC（含边界）内一点，点P到三角形边AB，BC，AC的距离为d1，d2，d3，求d1+d2+d3的取值范围．

如图，已知点P是三角形ABC外一点，且，，，．

（1）求证：；

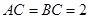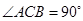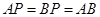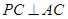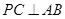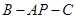（2）求二面角的大小；

 

 

已知P是三角形ABC内一点，且满足,则P为三角形ABC的（     ）

A、垂心          B、重心        C、内心           D、外心

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网