题目内容
1.已知椭圆C:$\frac{x^{2}}{a^{2}}$+$\frac{y^{2}}{b^{2}}$=1(a>b>0)的左、右焦点为F1、F2,离心率为e,点P(x0,y0)在曲线C上,且不与左、右顶点重合,设∠F1PF2=α,|PF1|=r1,|PF2|=r2,|OP|=r.(1)求证:①cosα≥1-2e2;②$\frac{1}{r_{1}}$+$\frac{1}{r_{2}}$≥$\frac{2}{a}$;③b≤r≤a(运用参数方程)
(2)若存在某点P使α=120°,${S}_{{△F}_{1}{PF}_{2}}$=4$\sqrt{3}$,曲线与圆x2+y2=36内切,求点P的坐标.
分析 (1)如图所示,①在△F1PF2中,由余弦定理可得:cosα=$\frac{{r}_{1}^{2}+{r}_{2}^{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$=$\frac{({r}_{1}+{r}_{2})^{2}-2{r}_{1}{r}_{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$=$\frac{4{a}^{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$-1,再利用基本不等式的性质与离心率计算公式即可得出;
②由r1+r2=2a,r1,r2>0,可得$\frac{1}{{r}_{1}}+\frac{1}{{r}_{2}}$=$\frac{1}{2a}({r}_{1}+{r}_{2})(\frac{1}{{r}_{1}}+\frac{1}{{r}_{2}})$,展开利用基本不等式的性质;
③设P(acosθ,bsinθ),(θ为参数),利用两点之间的距离公式可得:r=$\sqrt{{a}^{2}co{s}^{2}θ+{b}^{2}si{n}^{2}θ}$=$\sqrt{({a}^{2}-{b}^{2})co{s}^{2}θ+{b}^{2}}$,即可证明;
(2)由三角形的面积可得:r1r2.在△F1PF2中,由余弦定理可得:a2=4+c2,解得b2,由曲线与圆x2+y2=36内切,可得a=6,c2=32.F$(±4\sqrt{2},0)$.可得椭圆C的方程为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{4}$=1.联立$\left\{\begin{array}{l}{{r}_{1}{r}_{2}=16}\\{{r}_{1}+{r}_{2}=12}\end{array}\right.$,解得r1,r2.设P(m,n),联立$\left\{\begin{array}{l}{\frac{{m}^{2}}{36}+\frac{{n}^{2}}{4}=1}\\{\sqrt{(m-4\sqrt{2})^{2}+{n}^{2}}=6-2\sqrt{5}}\end{array}\right.$,解得即可.
解答 (1)证明:如图所示,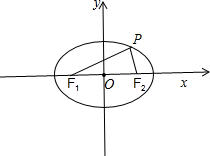
①在△F1PF2中,由余弦定理可得:
cosα=$\frac{{r}_{1}^{2}+{r}_{2}^{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$=$\frac{({r}_{1}+{r}_{2})^{2}-2{r}_{1}{r}_{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$=$\frac{4{a}^{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$-1$≥\frac{4{a}^{2}-4{c}^{2}}{\frac{({r}_{1}+{r}_{2})^{2}}{2}}$-1=$\frac{4{a}^{2}-4{c}^{2}}{2{a}^{2}}$1-2e2,当且仅当r1=r2=a时取等号;
②∵r1+r2=2a,r1,r2>0,
∴$\frac{1}{{r}_{1}}+\frac{1}{{r}_{2}}$=$\frac{1}{2a}({r}_{1}+{r}_{2})(\frac{1}{{r}_{1}}+\frac{1}{{r}_{2}})$=$\frac{1}{2a}(2+\frac{{r}_{1}}{{r}_{2}}+\frac{{r}_{2}}{{r}_{1}})$$≥\frac{1}{2a}(2+2\sqrt{\frac{{r}_{1}}{{r}_{2}}•\frac{{r}_{2}}{{r}_{1}}})$=$\frac{2}{a}$,当且仅当r1=r2=a时取等号;
③设P(acosθ,bsinθ),(θ为参数),
∴r=$\sqrt{{a}^{2}co{s}^{2}θ+{b}^{2}si{n}^{2}θ}$=$\sqrt{({a}^{2}-{b}^{2})co{s}^{2}θ+{b}^{2}}$$≥\sqrt{{b}^{2}}$=b,又r≤$\sqrt{{a}^{2}-{b}^{2}+{b}^{2}}$=a,
∴b≤r≤a.
(2)解:∵S△F1PF2=4$\sqrt{3}$,∴$\frac{1}{2}{r}_{1}{r}_{2}sin12{0}^{°}$=$4\sqrt{3}$,化为r1r2=16.
在△F1PF2中,由余弦定理可得:4c2=${r}_{1}^{2}+{r}_{2}^{2}$-2r1r2cos120°=$({r}_{1}+{r}_{2})^{2}$-r1r2=4a2-r1r2,
∴4a2=16+4c2,化为a2=4+c2,解得b2=4,
∵曲线与圆x2+y2=36内切,∴a=6,∴c2=32.F$(±4\sqrt{2},0)$.
∴椭圆C的方程为:$\frac{{x}^{2}}{36}+\frac{{y}^{2}}{4}$=1.
联立$\left\{\begin{array}{l}{{r}_{1}{r}_{2}=16}\\{{r}_{1}+{r}_{2}=12}\end{array}\right.$,解得$\left\{\begin{array}{l}{{r}_{1}=6+2\sqrt{5}}\\{{r}_{2}=6-2\sqrt{5}}\end{array}\right.$,或$\left\{\begin{array}{l}{{r}_{1}=6-2\sqrt{5}}\\{{r}_{2}=6+2\sqrt{5}}\end{array}\right.$.
设P(m,n),则$\left\{\begin{array}{l}{\frac{{m}^{2}}{36}+\frac{{n}^{2}}{4}=1}\\{\sqrt{(m-4\sqrt{2})^{2}+{n}^{2}}=6-2\sqrt{5}}\end{array}\right.$,
解得$(\frac{9\sqrt{2}-6\sqrt{7-3\sqrt{5}}}{2},±\frac{6\sqrt{5}+6\sqrt{14-6\sqrt{5}}-15}{2})$,
因此可得P:±$(\frac{9\sqrt{2}-6\sqrt{7-3\sqrt{5}}}{2},±\frac{6\sqrt{5}+6\sqrt{14-6\sqrt{5}}-15}{2})$.
点评 本题考查了椭圆与圆的标准方程及其性质、余弦定理、基本不等式的性质、椭圆的参数方程,考查了推理能力与计算能力,属于难题.

| A. | ax<bx | B. | xa>xb | C. | logxa>log${\;}_{{x}^{2}}$b | D. | logax>logbx |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,正方体A1B1C1D1-ABCD中,E,F分别是AD,BC1的中点.
如图,正方体A1B1C1D1-ABCD中,E,F分别是AD,BC1的中点. 如图所示,AD⊥平面ABC,CE⊥平面ABC,AD与 CE不相等,AC=AD=AB=1,BC=$\sqrt{2}$,四棱锥B-ACED的体积为$\frac{1}{2}$,F为BC的中点.求:
如图所示,AD⊥平面ABC,CE⊥平面ABC,AD与 CE不相等,AC=AD=AB=1,BC=$\sqrt{2}$,四棱锥B-ACED的体积为$\frac{1}{2}$,F为BC的中点.求: