题目内容
(本小题满分12分)已知数列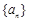 、
、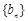 满足
满足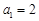 ,
,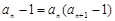 ,
,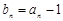 。
。
(Ⅰ)求数列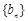 的通项公式;
的通项公式;
(II)求数列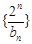 的前n项和
的前n项和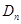 ;
;
(III)若数列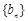 的前
的前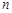 项和为
项和为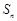 ,设
,设
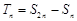 ,求证:
,求证: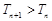 。
。
【答案】
解:(1)由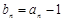 得
得 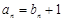 代入
代入 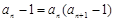 ,
,
得 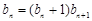 ,整理得
,整理得
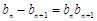 。﹍﹍﹍﹍﹍﹍﹍﹍2分
。﹍﹍﹍﹍﹍﹍﹍﹍2分
∵ 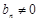 , 否则
, 否则 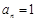 ,与
,与
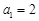 矛盾。
矛盾。
从而得 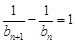 ,
,
∵ 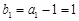 ∴数列
∴数列
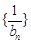 是首项为1,公差为1的等差数列。﹍4分
是首项为1,公差为1的等差数列。﹍4分
∴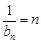 ,即
,即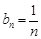 .--------------------------------------------------------------6分
.--------------------------------------------------------------6分
(2)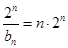
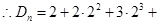 ┄┄+
┄┄+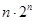 (1)
(1)
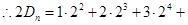 ┄┄+
┄┄+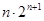 (2)﹍﹍﹍﹍﹍﹍﹍6分
(2)﹍﹍﹍﹍﹍﹍﹍6分
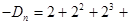 ┄┄
┄┄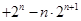
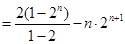
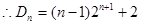 .┄┄┄┄┄┄┄┄┄┄┄8分
.┄┄┄┄┄┄┄┄┄┄┄8分
(3)∵
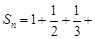 ……
……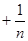 ,
,
∴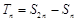 =(
=(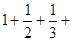 ……
……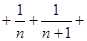 ……
……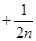 )—
)—
(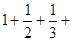 ……
……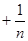 )=
)=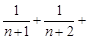 ……
……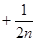 。﹍﹍﹍﹍﹍12分
。﹍﹍﹍﹍﹍12分
证法1:∵ 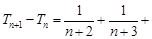 ……
……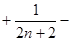 (
(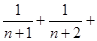 ……+
……+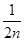 )
)
=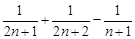 =
=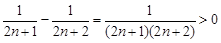
∴ .--------------------------------------------------------------14分
.--------------------------------------------------------------14分
证法2:∵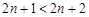 , ∴
, ∴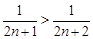 ,
,
∴ 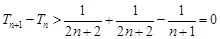 。
。
∴ .---------------------------------------------------------------12分
.---------------------------------------------------------------12分
【解析】略

练习册系列答案
相关题目