题目内容
在边长为4的正方形ABCD中，沿对角线AC将其折成一个直二面角B-AC-D，则点B到直线CD的距离为（ ）
A、2
| ||
B、2
| ||
C、3
| ||
D、2+2
|
分析：先找出二面角B-AC-D的平面角，根据直二面角的定义可求出BD的长，从而得到三角形BCD为等边三角形，则CD边上的中线即为点B到直线CD的距离，求出BF即可．
解答：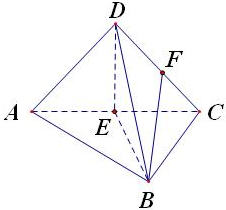
解：取AC的中点E，连接DE、BE，取CD的中点F，连接BF
根据正方形的性质可知DE⊥AC，BE⊥AC，
则∠BED为二面角B-AC-D的平面角，则∠BED=90°
而DE=BE=2
，则BD=4，而BC=DC=4
∴三角形BCD为等边三角形即BF⊥CD
∴点B到直线CD的距离为BF=2
故选：B．
解：取AC的中点E，连接DE、BE，取CD的中点F，连接BF根据正方形的性质可知DE⊥AC，BE⊥AC，
则∠BED为二面角B-AC-D的平面角，则∠BED=90°
而DE=BE=2
| 2 |
∴三角形BCD为等边三角形即BF⊥CD
∴点B到直线CD的距离为BF=2
| 3 |
故选：B．
点评：本题主要考查了直二面角的应用，以及点到平面的距离的求解，同时考查了空间想象能力、推理能力和计算能力，属于基础题．
练习册系列答案
相关题目
如图，在边长为4的正方形ABCD上有一点P，沿着折线BCDA由B点（起点）向A点（终点）移动，设P点移动的路程为x，△ABP的面积为y=f（x）．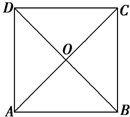
如图所示，在边长为4的正方形纸片ABCD中，AC与BD相交于O，剪去△AOB，将剩余部分沿OC、OD折叠，使OA、OB重合，则以A、（B）、C、D、O为顶点的四面体的体积为
应用题
如图，在边长为4的正方形ABCD的边上有一动点P，沿折线BCDA由点B（起点）向点A（终点）移动，设点P移动的路程为x，△APB的面积为y．