题目内容
 应用题
应用题如图所示,在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA,由B(起点)向点A(终点)运动,设点P运动路程为x,△ABP的面积为y,求
(1)y与x之间的函数关系式;
(2)画出y=f(x)的图象,并写出其单调区间及值域.
分析:(1)先求出定义域,然后根据点P的位置进行分类讨论,根据三角形的面积公式求出每一段△ABP的面积与P移动的路程间的函数关系式,最后用分段函数进行表示即可;
(2)根据每一段的函数解析式画出每一段的函数图象,结合函数图象即可求出函数的单调区间及值域.
(2)根据每一段的函数解析式画出每一段的函数图象,结合函数图象即可求出函数的单调区间及值域.
解答:解:(1)由于x=0与x=12时,三点A、B、P不能构成三角形,故这个函数的定义域为(0,12).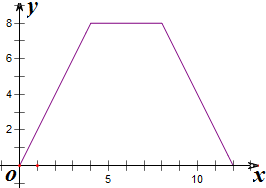
当0<x≤4时,S=y=
•4•x=2x;
当4<x≤8时,S=y=8;
当8<x<12时,S=y=
•4•(12-x)=2(12-x)=24-2x.
∴这个函数的解析式为
y=
;
(2)y=f(x)的图象为右上图,
由图知函数在(0,4]上单调递增,在(4,8)无单调性,在(8,12)上单调递减,
函数y=f(x)的值域为(0,8].

当0<x≤4时,S=y=
| 1 |
| 2 |
当4<x≤8时,S=y=8;
当8<x<12时,S=y=
| 1 |
| 2 |
∴这个函数的解析式为
y=
|
(2)y=f(x)的图象为右上图,
由图知函数在(0,4]上单调递增,在(4,8)无单调性,在(8,12)上单调递减,
函数y=f(x)的值域为(0,8].
点评:本题主要考查了函数解析式的求解,以及分段函数的图象等有关基础知识,分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目