题目内容
(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知函数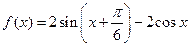 ,
, 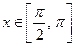 .
.
(1)若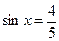 ,求函数
,求函数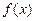 的值;
的值;
(2)求函数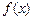 的值域.
的值域.
(1)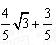 (2)
(2)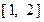
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
(本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知函数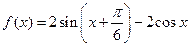 ,
, 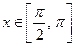 .
.
(1)若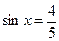 ,求函数
,求函数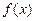 的值;
的值;
(2)求函数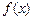 的值域.
的值域.
(1)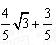 (2)
(2)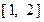
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案