题目内容
若一动点M与定直线l:x=
及定点A(5,0)的距离比是4:5.
(1)求动点M的轨迹C的方程;
(2)设所求轨迹C上有点P与两定点A和B(-5,0)的连线互相垂直,求|PA|•|PB|的值.
| 16 | 5 |
(1)求动点M的轨迹C的方程;
(2)设所求轨迹C上有点P与两定点A和B(-5,0)的连线互相垂直,求|PA|•|PB|的值.
分析:(1)欲求轨迹C的方程,设动点M(x,y),充分利用题设条件转化为坐标表示即可;
(2)利用(1)中结论,利用双曲线的定义结合垂直条件得到的直角三角形,即可求得|PA|•|PB|的值.
(2)利用(1)中结论,利用双曲线的定义结合垂直条件得到的直角三角形,即可求得|PA|•|PB|的值.
解答:解:(1)设动点M(x,y),
根据题意得
=
,
化简得9x2-16y2=144,
即
-
=1.
(2)由(1)知轨迹C为双曲线,A、B即为C的两个焦点,
∴|PA|-|PB|=±8.①
又PA⊥PB,∴|PA|2+|PB|2=|AB|2=100.②
由②-①2得|PA|•|PB|=18.
根据题意得
|x-
| ||
|
| 4 |
| 5 |
化简得9x2-16y2=144,
即
| x2 |
| 16 |
| y2 |
| 9 |
(2)由(1)知轨迹C为双曲线,A、B即为C的两个焦点,
∴|PA|-|PB|=±8.①
又PA⊥PB,∴|PA|2+|PB|2=|AB|2=100.②
由②-①2得|PA|•|PB|=18.
点评:求曲线的轨迹方程是解析几何的基本问题.求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系.

练习册系列答案
相关题目
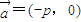 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求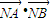 的最小值.
的最小值.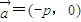 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求 的最小值.
的最小值.